現在我們瞭解了各種保存密鑰的方法,但在這些方法裡,我們總是把密鑰保存在一個地方:要麼鎖在保險箱,要麼保存在軟件中或打印在紙上。這會造成一個問題:一毀俱毀。當然,我們可以為密鑰建立備份,這可以降低密鑰丟失或損壞的風險(可獲取性),但同時會增加密鑰被盜的風險(安全性)。那是否存在一種方法,可以使密鑰的可獲取性和安全性都得到提高?答案是肯定的。密碼學上有一種稱為「密鑰分存」的技術,就可以做到這一點。
方法如下:密鑰被分成N個片段,只要我們獲得其中的K個片段,就可以把原密鑰重新還原。但如果獲得的片段數量少於K,就無法知道關於密鑰的任何信息。
要實現上述效果,把密鑰簡單地切分成若干片段是不行的,這樣的話,每一個片段都會透露密鑰的部分信息。[1]所以,密鑰分存並不是簡單地切分密鑰,而是將密鑰轉換成若干「子密鑰」。
舉個例子,我們設定N=2,K=2,意味著我們把想要加密的密鑰(原密鑰)轉換成兩個子密鑰,只有同時獲得這兩個子密鑰才能拼出原密鑰。我們把原密鑰稱為S,S是一個很大的數字(比如128位)。然後,我們可以隨機產生另一個128位的數字R,讓R作為其中的一個子密鑰,那麼另外一個子密鑰就是S⊕R(⊕代表邏輯算符互斥,exclusive OR,或縮寫成XOR,也叫異或),我們把S⊕R稱為「密文」。然後,我們把子密鑰R和密文S⊕R保存在兩個不同的地方。單獨根據子密鑰R或密文都無法知曉原來密鑰的任何信息,但如果我們同時得到R和S⊕R,我們可以通過異或邏輯運算得到原來的密鑰。[2]
N和K相等時,我們總是可以這樣做:對於之前的K-1個子密鑰,我們可以生成N-1不同的隨機數,最後一個子密鑰就是原密鑰與所有其他N-1個子密鑰的異或。但如果N大於K的話,這個技巧就行不通了。我們需要借助其他代數方法。
圖4.4中,我們是如何生成子密鑰的呢?首先,我們把S標記在Y軸上(0,S),然後經過該點畫一條直線,斜率隨機,接下來,我們就可以在這條線上挑一些點,要多少有多少。這樣,我們就得到N個子密鑰,並且K=2。
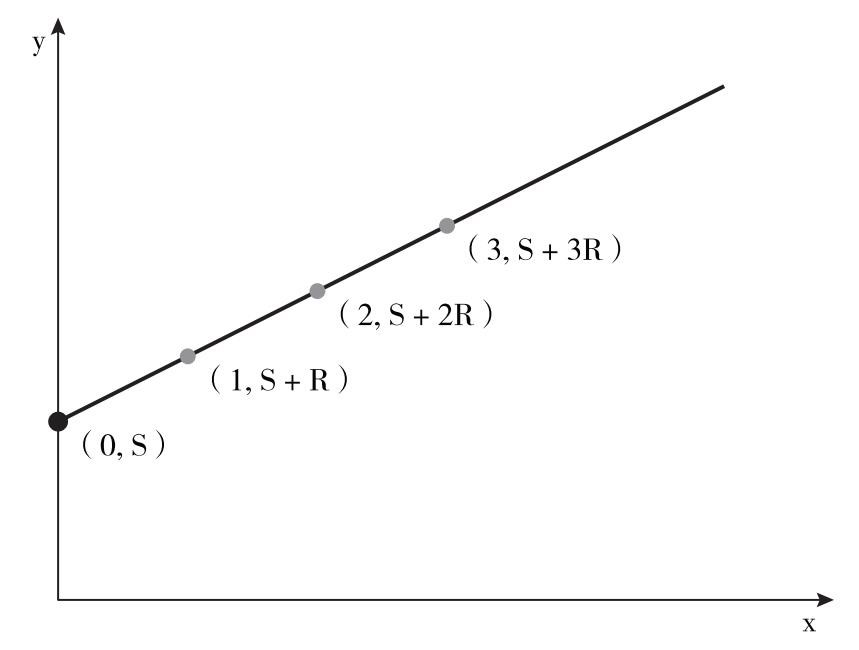
圖4.4 密鑰分存的幾何示例(N=2)
註:S代表原密鑰,被編碼成一個大的整數,圖中斜線的斜率隨機。斜線上的點(主要是它們的Y坐標S+R,S+2R,…)代表子密鑰。連接任何兩個點,都可以得到S[兩點連線,延長,與Y軸的交點就是S(黑點)]。若是只有一個點,又無法確定斜率(斜率隨機),就無法得到S。加 入 會 員 微 信
為什麼我們得到兩個點就可以還原原密鑰呢?首先,連接兩個點可以得到一條直線,這條直線和Y軸的交點就是S。然而,如果只有一個點,將得不到任何信息,由於直線斜率是隨機的,所以,通過該點的任何直線都有可能是我們生成子密鑰所採用的那條直線,但所有直線和Y軸的交點都不同。
上述方法中,有一點很精妙:要讓這個方法在數學上行得通,我們需要找一個足夠大的素數P取模。P不需要和原密鑰有任何關係,只需要足夠大就可以。S的值在0和P-1之間(含0和P-1)。上文中,我們說通過S畫直線並在直線上挑選一些點,實際操作時,我們其實是生成一個介於0到P-1的隨機數R,並生成下列點:
x=1,y=(S+R)mod P
x=2,y=(S+2R)mod P
x=3,y=(S+3R)mod P
原密鑰對應的坐標為x=0,y=(S+0×R) mod P,其實就x=0,y=S。
上述方法在K=2,N為任意數字的情況下都有效,例如,如果N=4,就是生成4個子密鑰,並保存在4個不同的設備裡。萬一有人偷了其中的一個,他對密鑰仍一無所知。即使丟了兩個子密鑰,你也仍然可以通過另外兩個子密鑰來得到原密鑰。
上述方法可以進一步擴展:我們可以用任何的K和N(只要保證K<N)來實現密鑰分存。在圖4.4中我們用一條直線進行密鑰分存,在代數中,直線就是自由度為1的多項式。如果K=3,我們就要用拋物線來實現,拋物線是自由度為2的多項式。我們可以用表4.1中所示公式來表達這一遞進系列。
表4.1 密鑰分存的數學原理

注意,如果使用自由度為k-1的曲線上的若幹點來進行密鑰分存,那麼,為了還原原密鑰,至少需要得到K個點的數據。
數學上,拉格朗日公式表明,如果要回歸一條自由度為k-1的曲線,需要獲得至少K個點。最簡單的例子就是,用尺子連接兩個點,就可以得到一條直線。因此,如果我們將原密鑰轉換成N個子密鑰,除非黑客獲得了K-1個子密鑰,否則原密鑰就是安全的,換個說法,我們最多可以承受N-K個子密鑰被洩露。
當然,密鑰分存並不是比特幣的專用技術。你可以將你的密碼進行密鑰分存,然後把子密鑰告訴你的朋友,或把它們放在不同的地方。但是,實際上並不會有人真的這麼做。一方面這麼做不太方便,另一方面,目前市場上也有其他的安全機制,例如使用短信進行雙重驗證。但對於比特幣而言,如果你選擇本地保存密鑰,那麼雙重驗證等安全機制就不適用了,我們無法通過短信驗證碼的方式來控制比特幣賬戶。當然,在線錢包則不同,我們會在下一節討論。不過,在線錢包和本地儲存的區別不大,類似的問題總是存在,只不過換了一種方式。畢竟,在線錢包的服務商在保存密鑰的時候也不能只使用一種安全措施。
門限密碼(threshold cryptography)
密鑰分存還是有一個問題:密鑰分存之後,如果我們後面要用原密鑰來簽名,那就需要取得子密鑰,還原成原密鑰,然後才能簽名。這個過程有可能被黑客乘虛而入,盜取密鑰。
密碼學可以解決這個問題。如果子密鑰儲存在不同的設備中,可以以去中心化的方式還原原密鑰,而不是在某台設備上完成。這種技術叫「門限簽名」(threshold signature)技術。典型的例子就是使用雙重安全機制的電子錢包(N=2且K=2),如果兩個子密鑰分別保存在個人電腦和手機上,你可以在電腦上發起付款,這時,電腦會生成一個簽名片段,並發送到你的手機上,然後,手機會提示你付款信息(包括收款人、金額等),然後等待你確認。如果你確認了付款信息,這時,手機會利用它的子密鑰完成整個簽名,然後廣播到區塊鏈上。萬一黑客控制了你的電腦,試圖把比特幣轉到他的賬戶,你根據手機上的付款信息就知道有問題了,從而不會確認這筆交易。門限密碼涉及的數學細節比較複雜,此處我們不展開討論。
 門限簽名
門限簽名
門限簽名是密碼學中的一項技術,將一個密鑰切分成不同片段,分別儲存,在交易簽名時無須還原原密鑰。而多重簽名是比特幣腳本的特性,把一個比特幣賬戶的控制權交給多個密鑰,這些密鑰共同保障賬戶安全。門限簽名和多重簽名都能克服密鑰單點保存的缺陷。
多重簽名
還有另外一種方法可以克服密鑰單點保存的缺陷,即多重簽名(multisignatures),這個名詞在第3章曾出現過。通過比特幣腳本,可以直接把一個比特幣賬戶的控制權交給多個密鑰,而不是將密鑰分存。這些密鑰可以保存在不同的地點,並分別生成簽名。當然,最終完成的交易的信息還是會保存在某台設備上,但即使黑客控制了這台設備,他所能做的也只不過阻止這個交易被廣播到整個網絡上去。沒有其他設備參與,他無法生成出一個正當有效的多重簽名。
舉例來說,假設本書的作者安德魯(Andrew)、阿爾文德(Arvind)、愛德華(Ed)、約什(Joseph)和史蒂文(Steven)是一家公司的創始人——也許我們就是依靠出售這本書的版權來創建公司——那這家公司就有許多的比特幣了。我們可能會用多重簽名來保護這些比特幣。我們5個人,每人都有一對密鑰,我們可以用其中的3個簽名來保護冷儲存——一筆交易需要5個人中至少3個人的簽名才能完成。
這樣,只要我們5個人在不同地方且使用不同的安全措施保存各自的密鑰,那麼比特幣就會相當安全。黑客必須盜取我們當中3個人的密鑰,才能盜取比特幣。即便我們其中一個或兩個背棄了我們,他(們)也無法卷款而逃,因為他們還需要另一個簽名。[3]同時,如果我們其中一個遺失了密鑰,其他人還是可以取出比特幣,並轉到新的賬戶,重新設置密碼。總而言之,多重簽名可以比較妥善地管理在冷儲存端的大額比特幣,任何重大事項都需要多人的參與才能實現。
上文中,我們說到,人們使用門限簽名技術的原因是為了實現雙重安全機制或多重安全機制,使用多重簽名技術的原因是為了實現多人對共同財產實現共同控制。實際上,這兩種技術都可以實現上述兩種目的。
[1] 《鹿鼎記》裡的藏寶圖儲存方法在現實中是不可取的,因為不需要搜集齊八旗手中的碎片,只需要有幾旗的就可以猜出整個藏寶圖。——譯者注
[2] 在密碼學中,上文的「原密鑰」通常稱為「明文」,「R」稱為「密鑰」,S⊕R稱為「密文」。——譯者注
[3] 用這個方法倒是可以防止銀行工作人員卷款而逃,可見科技的進步確實可以改善傳統行業的一些薄弱環節。——譯者注
