演繹推理和歸納推理
我們已經知道,一個論證由做出某種斷言的結論和一個或多個用來支持該結論的前提組成。但是,支持有兩種不同的方式,這取決於前提是旨在確保結論的真,還是僅給結論提供某些理由。粗略地看,兩者之間的區別是:前者是一個決定性的關係,後者是一個非決定性的關係。不過,現在我們可以做更準確的區分:前提和斷言之間的決定性關係是演繹論證的一個標誌,而前提和斷言之間的非決定性關係是歸納論證的標誌。任何論證都是這兩種關係中的一種。
對於一個演繹論證來說,其結論可以從前提必然得出。下面是演繹論證的一些例子:
例4-9 1. 如果今天是星期一,那麼我們要上邏輯課。
2. 今天是星期一。
3. 我們要上邏輯課。
例4-10 1.所有的狗都會叫。
2.菲多是一隻狗。
3. 菲多會叫。
例4-11 1. 今天多雲並且溫暖。
2. 今天多雲。
對於這裡的每一個論證,如果前提都是真的,那麼結論也必定為真(不可能為假)。
所以,它們顯然都是演繹論證。再來看下面的例子:
例4-12 1.大多數大學生學過平面幾何。
2.這個班的有些學生學過平面幾何。
例4-13 1.很多貓是家養的。
2. 菲利克斯是一隻貓。
3. 菲利克斯是家養的。
對於例4-12和例4-13的論證,其前提至多都只提供了非決定性的理由:都不能保證其所支持的結論為真。即使前提為真,每一個論證的結論都可能為假。因此,我們把這類論證看作歸納性的。
分析論證時,記住圖4-1中的區分是很有幫助的。我們必須判斷一個給定的論證是演繹的還是歸納的,因為評估的標準也相應地不同。對於一些論證,如果被判定為演繹的,它們是有缺陷的;而如果被判定為歸納的,則是可行的。如果不能明確做出判斷,我們應該怎麼做?只要問問自己:前提為真能保證結論為真嗎?如果能,那麼最好就判定該論證是演繹的,並且用演繹論證的標準來分析。否則,看這些前提是否只是給結論提供了某些理由,使得即使所有前提都為真,結論也仍然可能為假?如果是,最好判定該論證為歸納性的,並且用歸納論證的標準來分析。演繹論證或歸納論證的標準是後面兩章的內容。
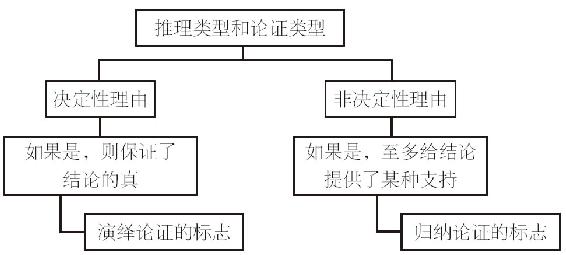
圖4-1 演繹論證和歸納論證