本文1930年首次發表於《哲學論壇》(Forum Philosophicum),比目前的文章長。最後的部分是談論場理論的最新進展的,但應愛因斯坦的要求,1953年德文版《我的世界觀》將這一部分刪掉了,原因是「當時的理論早就被拋棄了,代之以非對稱性的場論,而後者完全滿足邏輯—形式關係」。新的理論後來被愛因斯坦以附錄II的形式放在《相對論意義》(Meaning of Relativity, Princeton University Press, 1953)一書中。
本文參考1934年德文版《我的世界觀》,依據1954年英文版《觀念與見解》譯出。
科學思想是前科學思想的發展。由於在後者中,空間概念已經是基本的概念,我們必須從前科學思想中的空間概念開始講起。有兩種看待概念的方式,它們對理解都是必不可少的。第一種是邏輯分析,它回答了以下問題:概念和判斷怎樣互相依存?回答這個問題時,我們相對有底氣。答案是數學中的必然性,對此我們印象深刻。可是,獲得這種必然性是以內容的空虛為代價的。只有用感知的經驗把概念關聯起來,無論是怎樣間接的關聯,概念才能獲得內容。但是,邏輯思考不能揭示出這種關聯,只能通過經驗。然而,正是這種關聯決定了概念系統的認知價值。
舉例來說,設想在未來文明中,有一位考古學家,找到一本沒有圖解的歐幾里得幾何課本。他將發現命題中如何使用「點」「直線」「面」這幾個詞,也將認識到如何互相推導命題。他甚至能根據認識到的規則去構建新的命題。但是,只要「點」「直線」「面」等詞沒有向他表達什麼內容,那麼構建這些命題對他來說仍是空洞的文字遊戲。只有當它們確實意味著某些東西時,幾何學對他來說才具備真實的內容。這對於分析力學來說同樣是對的,甚至對於一門邏輯演繹科學的任何闡述來說都是對的。
當我們用「點」「直線」「面」來表達某些東西時,這是什麼意思?它的意思是,人們能指出這些詞所指的感覺經驗。這個超邏輯問題是幾何學的本質問題,考古學家只能憑直覺去解決它,通過檢查自己的經驗,看能不能發現一些東西,以對應那些理論的主要術語和為術語制定的公理。只有在這個意義上,才能合理地提出一個概念化實體的本質問題。
對於前科學的各個概念,我們在本體論問題上所處的位置與考古學家非常像。也就是說,我們已經忘記了是哪些經驗世界的特徵使得我們建構了那些概念;不戴上舊有的概念解釋的眼鏡,我們很難回想起經驗世界。更大的困難是:我們的語言被迫使用和那些原始概念緊密相關的詞語。這些是當我們試圖描述前科學中空間概念的本質時所面臨的障礙。
在我們轉向空間問題之前,對所有概念要注意的一點是:概念雖然涉及感覺經驗,但在邏輯意義上,它從來不是從感覺經驗中推導出來的。由於這個原因,我始終不能理解為何要尋求康德意義上的先驗。在任何本體論問題中,我們只想在複雜的感覺經驗中找出概念指代的那些特徵。
現在考慮空間概念:這似乎是以固體概念為前提的。固體概念的產生原因可能是複雜的意識組合和感覺印象,人們經常描述它們的本質。某些視覺和觸覺印象之間存在著聯繫,這些視覺和觸覺印象能被持續地追蹤,在任何時候都能被重現(觸覺、視覺),就是一些這樣的特徵。一旦通過上述經驗關係形成固體概念——這一固體概念絕不是以空間概念或空間關係概念為前提的——那麼要想從理性上把握這些固體間關係的要求,就必然會引出關於它們空間關係的一些概念。兩個固體可能是接觸的,也可能是分開的。在分開的固體中間,人們能將第三個物體插入而不引起二者的任何變化,但在接觸的固體間就不行。這些空間關係顯然和物體本身一樣都是真實的。如果兩個物體能同樣填滿一個這樣的間隔,那它們也能同樣填滿其他間隔。由此看出,間隔獨立於其填充物的具體選擇;這是空間關係的普遍真理。這種獨立性是構建純粹幾何學概念的實用意義的主要條件,很顯然沒有必要是先驗的。在我看來,這樣的間隔概念擺脫了填充物的具體選擇,是整個空間概念的出發點。
然後,我們從感覺經驗的觀點來看,按照上面的簡要說明,空間概念的發展似乎符合下面的模式——固體,固體的空間關係,間隔,空間。這樣看來,空間似乎和固體一樣,是某種實在。
人們很清楚,空間概念作為真實事物已經存在於科學之外的概念世界。然而,歐幾里得數學卻完全不涉及這樣的空間概念;它將自己限制在物體和物體間的空間關係這些概念中。點、面、直線、線段是理想化的物體。所有空間關係被簡化為接觸關係(直線和平面的相交、點在直線上等等)。作為一個連續統一體的空間,在概念系統中根本沒有出現。笛卡兒在用坐標描繪空間中的點時,首次提出空間這個概念。幾何圖像在這裡首次在某種形式上作為無限空間的一部分出現,這個無限空間被構思成一種三維連續統一體。
笛卡兒式空間處理的巨大優越性,絕不只在將分析應用於幾何學。主要一點倒像是:希臘人偏愛用特殊物體(直線、平面)來做幾何學描述;描述其他物體(比如橢圓),只有借助點、直線和平面來構造或定義。但在笛卡兒的方法中則不同,比如說一切平面在原理上的地位是平等的,在幾何學的構建中,對線性結構沒有任何主觀武斷的偏向。
幾何學被構思成支配實際剛體彼此之間空間關係規律的科學。就此來說,它應當被看作物理學最古老的分支。正像我提到的,這門科學無須這樣的空間概念,理想的物質形式——點、直線、面、線段——就足夠滿足它的要求了。笛卡兒構想的整個空間,對牛頓物理學來說是絕對必要的,因為動力學不能只靠質點概念和(隨時間變化的)質點間距離。在牛頓運動方程中,加速度概念扮演了根本性角色,它不能只用隨時間變化的點間間隔去定義。
只有把空間當作整體,才能構想或者定義牛頓的加速度。因此,除空間概念的幾何實在以外,空間多了一個決定慣性的新功能。當牛頓描繪絕對空間時,無疑是指空間的這一實在意義。他必須將這種意義歸於一種十分確定的運動狀態,但這種狀態看起來沒有被力學現象完全決定。這一空間的絕對性還有另一個意義;空間決定慣性被設想成是自發的,也就是說不受任何物理環境的影響;空間影響質量,但是不受任何東西影響。
直到最近,在物理學思想中,空間僅是所有事件的被動容器,它不參與物理事件。伴隨光的波動理論和法拉第、麥克斯韋的電磁場理論的誕生,思想才開始發生新的轉變。人們開始明白,自由空間中存在以波傳播自身的狀態,還有能對放入其中的帶電物質或磁極施力的定域場。因為對19世紀的物理學家來說,將物理作用或狀態歸因於空間自身完全是荒誕的,他們於是基於實質物質的模型發明了一種遍佈於整個空間的媒介物——以太,將其設想成電磁現象中的傳播媒介,因而也是光的傳播媒介。人們猜想這種媒介物構成了電磁場,並基於固體的彈性形變模型,一開始認為其狀態是機械性的。但是這個機械以太理論從沒有成功過,所以人們逐漸放棄了對以太場本質做更詳細的解釋。以太因此變成了一種起到電場基礎作用的物質,但是從本質上無法做更進一步的分析。於是有了下面的圖景:空間充滿以太,重量物質的微粒或原子在其中四處游動;物質的原子結構於世紀之交被穩固地建立起來了。既然物體的相互作用應該通過場完成,那麼在以太中也一定有引力場,然而那時的以太的引力定律還沒有明確的形式。人們只是把以太設想成是所有跨空間作用的力的場所。隨著人們認識到運動的帶電物質產生磁場,而磁場能量提供了一種慣性模型,慣性也似乎是以太中的一種定域的場作用。
起初,以太的力學性質是一個謎。不久,就出現了H. A.洛倫茲的偉大發現。那時所有已知的電磁現象都用以下兩個假設作為基礎加以解釋:第一個假設是以太牢牢地固定在空間中,也就是說,它一點兒也不能移動;第二個是電荷是牢固地附屬於移動的基本粒子。現在對洛倫茲的發現可以表述如下:物理空間和以太是同一事物的不同稱呼,場是空間的物理狀態。因為如果粒子的運動狀態不能歸因於以太,似乎沒有理由在空間之外引入一種這樣特殊的實體。但是物理學家仍和這樣的思維相去甚遠;對他們來說,空間仍是某種剛性均勻的東西,不能發生變化或擁有各種狀態。只有黎曼——這位孤獨的、不被理解的天才,在19世紀中葉發現了通往空間的新概念之路。新的空間概念不具備剛性,並且具有參與物理事件的可能性。
這一智力成就出現在法拉第和麥克斯韋電場理論之前,這越發令我們欽佩。然後出現了狹義相對論,它認為所有慣性繫在物理上是等價的。電動力學或者說光的傳播規律,揭示了時間和空間是不可分離的。在這之前,人們潛在假設:事件的四維連續統一體能以客觀的方式分解為時間和空間。也就是說,對所有事件來說,「現在」具有絕對的意義。利用同時的相對性這一發現,空間和時間被合併成一個完整統一的連續體,就像之前空間的三維合併成一個完整統一的連續體一樣。這樣,物理空間就擴展成一種含有時間維度的四維空間。狹義相對論的四維空間就像牛頓空間一樣,是剛性和絕對的。
狹義相對論很好地表現了理論科學現代發展的基本特徵。最初的假設一如既往地變得更加抽像和遠離經驗。而且,它更靠近一切科學的宏偉目標:從盡可能少的假設或公理出發,用邏輯推論去涵蓋盡可能多的經驗事實。同時,從公理通往經驗事實或可證結果的思想鏈條不斷加長,變得更不直接。理論科學家在探尋某種理論的過程中,被迫越來越依賴純數學的形式思考,因為實驗家的實際經驗不能引導他到達最高度抽像的境界。適合早期科學且處於支配地位的歸納法正讓位於實驗性的演繹法。必須對這樣的理論結構做徹底詳盡的考察,才能得出可以和經驗對比的結論。在這裡,觀測事實毫無疑問仍然是最高的仲裁者;但是在它做出裁決之前,必須經過反覆深刻的思考來跨過公理和可證實結論的鴻溝。著手這項極其艱巨的任務時,理論家必須完全意識到,他的努力可能最後只不過是為推翻自己的理論做準備而已。從事這樣一項工作的理論家不應該被吹毛求疵地說成是「異想天開」;相反,他應該有自由支配想像的權利,因為這是到達目標的唯一途徑。他的工作並不是無意義的白日做夢,而是尋找邏輯上最簡單的可能性及其後果。我在這裡做這個辯解,是為了使聽眾或讀者更願意關注隨後發生的一連串思考;這以思想脈絡從狹義相對論轉向廣義相對論,再由此轉向它最新的分支——統一場論。在這個論述中,我免不了會用到數學符號。
我們從狹義相對論開始。該理論仍以光速不變的經驗規律為直接基礎。假設P是真空中的一點,P'是距dσ無限接近的另一點。在t時刻從P點發出的光,於t+dt時刻到達P'。那麼有
dσ2=c2dt2
如果dx1、dx2、dx3是dσ的正交投射,並且引入虛時間坐標 ,那麼上述光速不變定律將採用下面的形式:
,那麼上述光速不變定律將採用下面的形式:
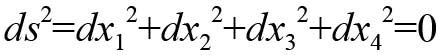
既然公式表達一種真實狀況,我們可以認為量ds具有物理意義,只要在四維連續體當中的相鄰點使得對應的ds不為零。它可做如下表述:狹義相對論(有虛時間坐標)的四維空間具備歐幾里得度規。
被稱為歐幾里得的度規,和下述事情有關。三維連續統一體中這種度規的假設,完全等價於歐幾里得幾何的公理假設。度規的定義方程正是應用於坐標微分的畢達哥拉斯定理(勾股定理)。
狹義相對論中允許的(通過變換的)坐標變化是這樣的,新坐標系中,量ds2(基礎不變量)等於坐標微分的平方之和。這樣的變換稱為洛倫茲變換。
狹義相對論的啟發性方法的特徵,就是下述原理:當用洛倫茲變換改變坐標,方程的形式不變時(方程在洛倫茲變換下的協變性),這樣的方程才被接受為自然規律的一個表達。
這個方法使我們發現以下的必然聯繫:動量和能量之間,電場力和磁場力之間,靜電力和電動力之間,慣性質量和能量之間。因此,物理中獨立概念和基本方程的數量就減少了。
這個方法超越了自身。表達自然規律的方程僅僅對洛倫茲變換有協變性,其他變換就不行,這一點是正確的嗎?好吧,用這種方式提問真是沒有意義,因為每個方程組都能用廣義坐標表述。我們須問:自然規律的表述,是不是本來就不應該因為選取了一組特定的坐標系而得到實質性的簡化?
我們只想順便說下,慣性質量和引力質量等價的這條經驗規律,提示我們對上面的問題給出肯定的回答。如果我們將為表達自然規律的所有坐標系的等效性提升到基本原理的高度,並保留光速不變原理,或者換句話說至少對於四維空間的無限小部分保留歐幾里得度規的客觀意義的假設,就得到廣義相對論。
這意味著對於空間的有限區域,可以根據下面的公式,假定存在一個(有物理意義的)廣義黎曼度規:

其中,所有的腳標μv組合都將從(1,1)到(4,4)取和。
與歐幾里得空間結構相比,這樣的空間結構在一個方面有根本不同。係數gμv暫時是坐標x1到x2的任意函數;實際上知道了這些函數gμv之後,才能真正確定空間結構。也可以說:這樣的空間結構完全是未定的。通過詳細說明度規場滿足的規律,才能更加確定空間結構。在物理層面上講,人們假設度規場同時也是引力場。
既然質量的分佈決定和改變引力場,空間的幾何結構也取決於物理因素。因此,根據這個理論,空間——正如黎曼猜想的——不再是絕對的;它的結構取決於物理的影響。(物理)幾何學不再像歐幾里得幾何那樣,是一門孤立的自足的科學了。
引力問題就這樣被簡化為數學問題:要找到最簡單的基本方程,它們與任意坐標變換都是協變的。這是一個十分明確,至少能被解決的難題。
我在這裡先不講這項理論的實驗驗證,但馬上會解釋為什麼該理論不能永遠滿足於這個成就。引力的確已經從空間結構演繹出來,但是除了引力場,還有電磁場。首先,電磁場必須作為獨立於引力的實體被引入理論。基本場方程中必須增加一個考慮電磁場存在的數學項。但是,理論精神是無法忍受存在度規—引力結構和電磁結構這兩種相互獨立的空間結構。這就促使我們相信,這兩種場必定符合某種統一的空間結構。
