我們需要理解的第一個密碼學的基礎知識是密碼學哈希函數,哈希函數是一個數學函數,具有以下三個特性:
● 其輸入可為任意大小的字符串。
● 它產生固定大小的輸出。為使本章討論更具體,我們假設輸出值大小為256位,但是,我們的討論適用於任意規模的輸出,只要其足夠大。
● 它能進行有效計算,簡單來說就是對於特定的輸入字符串,在合理時間內,我們可以算出哈希函數的輸出。更準確地說,對應n位的字符串,其哈希值計算的複雜度為O(n)。
這些特性定義了一般哈希函數,以這個函數為基礎,我們可以創建數據結構,例如哈希表。我們將只專注於加密的哈希函數,要使哈希函數達到密碼安全,我們要求其具有以下三個附加特性:(1)碰撞阻力(collision-resistance);(2)隱秘性(hiding);(3)謎題友好(puzzle-friendliness)。
我們會仔細研究這些特性,並會逐步闡釋我們為什麼需要這樣的函數。學習過密碼學的讀者可能會注意到,我們這裡對於哈希函數的論述與一般的密碼學課程會有所不同,特別是關於謎題友好。在一般密碼學中,謎題友好並非加密的哈希函數的一般要求,卻對加密數字貨幣這一特性非常有用。
特性1:碰撞阻力
加密的哈希函數的第一個特性是它要具有碰撞阻力。這裡的碰撞指對於兩個不同的輸入,產生相同的輸出。如果對於哈希函數H(·),沒有人能夠找到碰撞,我們則稱該函數具有碰撞阻力(見圖1.1)。即:
碰撞阻力 如果無法找到兩個值,x和y,x≠y,而H(x)=H(y),則稱哈希函數H具有碰撞阻力。
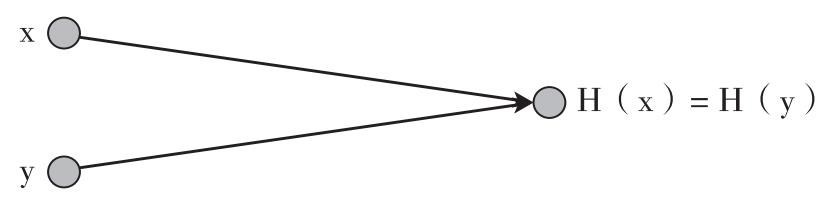
圖1.1 哈希碰撞
註:x和y分別是不同輸入,當作為哈希函數的輸入時,會產生相同的輸出。這時我們就說這個函數是哈希碰撞的。
注意,我們說沒人能找到碰撞,並不表示不存在碰撞。事實上,通過簡單的計數論證(counting argument),我們可以證明碰撞的確存在。哈希函數的輸入空間包含所有長度的任意字符串,但輸出空間則只包含特定固定長度的字符串。因為輸入空間比輸出空間大(輸入空間是無限的,而輸出空間是有限的),一定會有輸入字符串映射到相同的輸出字符串。實際上,根據鴿巢原理(Pigeonhole Principle),我們可以得出,必然會有大量可能的輸入被映射到任意特定輸出(見圖1.2)。加 入 會 員 微 信
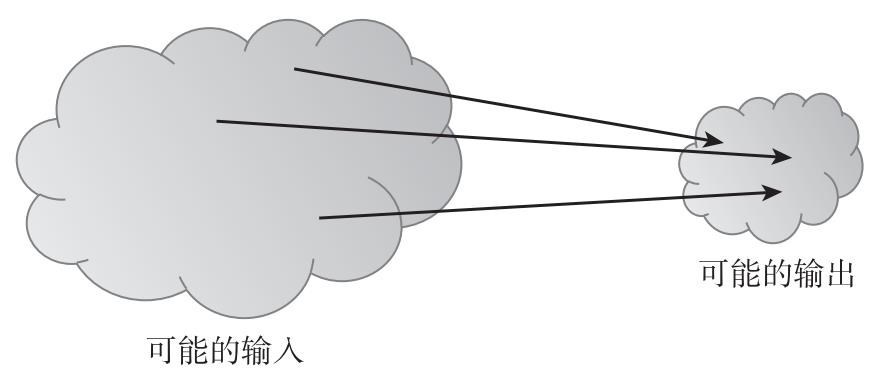
圖1.2 必然的碰撞
註:因為輸入的數量超過輸出的數量,我們可以確定某一個輸出肯定對應多個輸入。
而更糟糕的是,對於加密的哈希函數,我們雖然說應該找不到碰撞,但有些方法是能保證找到碰撞的。考慮以下對應於一個256位輸出大小的哈希函數,選擇2256+1個不同數值,計算每個數的哈希值,並檢查是否有兩個相等的輸出。因為我們這裡選擇的輸入多於輸出,因此在應用哈希函數時,一些數對必將產生碰撞。
使用上述方法一定能找到碰撞。但如果我們隨機性地選擇輸入,並計算哈希值,我們在檢驗第2256+1個輸入之前便很可能找到碰撞。實際上,如果我們隨機選擇2130+1個輸入值,找到至少兩個等同哈希值的概率為99.8%。僅僅通過檢驗可能輸出數量的平方根次數,便大體能找到碰撞,這一事實在概率學中被稱為是生日悖論(birthday paradox)[1]。
這個碰撞檢測算法對每個哈希函數都有效,但是它的問題是其計算需要花很長很長時間才能完成。對於一個256位輸出的哈希函數來說,最壞的情況是你需要進行2256+1次哈希函數計算,平均次數為2128次,這簡直是一個天文數字——如果一台電腦每秒計算10 000個哈希值,計算2128個哈希值,需要花1027多年時間!換個角度,我們可以說,如果人類製造的每台電腦在整個宇宙起源時便開始計算,到目前為止,它們找到碰撞的概率仍然無窮小,比下兩秒鐘地球將被大隕石摧毀的概率還要小得多。
因此,為了尋找一個任意的哈希函數的碰撞,我們只是有了一個一般,但並不實用的算法。一個更艱澀的問題是:有沒有其他的方法,可以用於對於某一特定哈希函數找到碰撞?也就是說,雖然一般的碰撞測試算法不適用,但仍可能有其他的算法,可以有效地找到某個哈希函數的碰撞。
以下面的哈希函數為例:
H(x)=x mod 2256
這個函數接受任何長度的輸入,產生一個固定大小輸出(256位),且能進行有效計算,因此符合我們對哈希函數的要求。但是對於這個函數,我們確實具備一個有效的能夠尋找碰撞的方法。注意,這個函數僅返回輸入的最後256位,因此,數值3和3+2256就構成了碰撞[2]。這個簡單的例子表明,雖然我們的一般碰撞測試方法在實踐中不可行,但至少對於某些哈希函數,存在有效的測試碰撞的方法。
但對於某些哈希函數,我們無法確認識別碰撞的有效方法是否存在,我們只是懷疑這些函數具有防碰撞特性,但是我們已經證明,世界上沒有哈希函數具有防碰撞特性。我們實踐中依賴的加密的哈希函數僅僅是人們經過不懈努力之後暫未成功找到碰撞的函數。因此,我們選擇相信那些加密的哈希函數具有哈希阻力(在某些情況下,如之前的MD5哈希函數,在多年的努力之後最終找到了碰撞,導致該函數在實踐中被逐漸淘汰,最終被棄用)。
應用:信息摘要
現在我們知道什麼是碰撞阻力了,我們自然會問:碰撞阻力有什麼用途?以下就是一個應用:哈希函數H具有碰撞阻力,x和y是兩個不同的輸入,那麼可以假設它們的哈希函數H(x)和H(y)也不同——如果已知x和y不同,但哈希值相同,那麼H具有碰撞阻力的假設就不成立了。
這個論證使我們可以將哈希輸出作為信息摘要(message digest)。以SecureBox為例,SecureBox是一個允許用戶上傳文件,並保證文件被完整下載的線上文件存儲系統。假設愛麗絲上傳了很大的文件,並希望能夠在之後下載時確認她下載的文件與她上傳的文件相同。一種方法是將整個文件進行本地存儲,並直接將其與下載文件對比。如果這樣可行,那麼將文件上傳便顯得毫無意義,倘若愛麗絲需要使用本地文件副本以保證其完整性,她可以直接使用本地副本。
無碰撞哈希函數為這個問題提供了簡單有效的解決方法,愛麗絲只需要記住原文件的哈希值,從SecureBox下載文件後,她可以計算下載文件的哈希值,並與原文件哈希值進行對比。如果哈希值相同,那麼愛麗絲可以說該文件就是她上傳的那一個,但是如果不同,她則可以確定文件被破壞了。記錄哈希值可以幫助愛麗絲檢測文件在傳輸過程中,或在SecureBox服務器上是否產生了意外損壞,或者檢測文件是否受到服務器的蓄意修改。保證主體不受其他實體的惡意行為侵害,這正是密碼學的核心。
這裡的哈希函數對於一個信息生成固定長度的摘要,或生成了簡明總結,這為我們提供了一種記住之前所見事物,並在今後認出這些事物的有效方法。雖然整個文件可能非常大,存儲規模達數G,但其哈希值的長度固定。例如,哈希函數為256位。這樣做,極大地降低了存儲要求。在本章後面及整本書中,我們都會看到哈希作為信息摘要的應用。
特性2:隱秘性
我們希望哈希函數擁有的第二個特性是其隱秘性。隱秘性保證,如果我們僅僅知道哈希函數的輸出y=H(x),我們沒有可行的辦法算出輸入值x。問題是,上述的表示形式不一定是正確的。考慮以下簡單的例子:我們做一個拋硬幣的實驗,如果拋硬幣結果為正面,我們會宣佈字符串哈希為「正面」;如果結果為反面,我們會宣佈字符串哈希為「反面」。
然後我們問我們的對手,在他沒有見到拋硬幣,而只見到哈希函數的輸出的前提下說出哈希函數的輸入字符串(很快我們就知道為什麼要玩這個遊戲了)。為了回答問題,對手會簡單計算「正面」字符串的哈希值及「反面」字符串的哈希值,然後對手便可以知道他得到的是哪一個。這樣,只需要幾步,對手就能反解出輸入值。
對手能夠猜出字符串,這是因為x只有兩個可能,他可以很輕易地將兩個可能對應的哈希值計算出來。為了能夠實現隱秘性,我們需要x的取值來自一個非常廣泛的集合,也就是說,僅僅通過嘗試幾個特定的x,就能找到輸出值的方式將不會發生了。
現在的問題是:在類似拋硬幣的「正面」、「反面」實驗中,如果我們想要的反解的輸入值並非來自分散的集合,我們是否還能得到隱秘性?幸運的是,對於這個問題答案是肯定的!我們甚至能夠通過與另一個較為分散的輸入進行結合,而將一個並不分散的輸入進行隱秘。現在我們可以更精確地表示隱秘的含義了(雙豎線∥為連接符號,代表把一系列事件、事情等聯繫起來)。
隱秘性 哈希函數H具有隱秘性,如果:當其輸入r選自一個高階最小熵(high min-entroy)的概率分佈,在給定H(r∥x)條件下來確定x是不可行的。
在信息論中,最小熵是用於測試結果可預測性的手段,而高階最小熵這個概念比較直觀描述了分佈(如隨機變量)的分散程度。具體來說,在從這樣分佈中取樣時,我們將無法判定取樣的傾向。舉個具體的例子,如果r是從長度為256位的字符串中隨意選出的,那麼任意特定字符串被選中的概率為1/2256,這是一個小到幾乎可以忽略的取值。
應用:承諾
現在來看一下隱秘性的應用。具體來說,我們把想做的事情稱為承諾(commitment)。這裡承諾是一個數字化過程,可以類比為以下動作:首先選定一個數字,將數字裝進信封,然後將該信封放到一個人人都看得到的桌子上。這樣做以後,可以說你就信封裡的數字做出了承諾,在打開信封前,雖然你已經做出了承諾,對其他人來說它還是秘密。在之後,你可以打開信封,來展示承諾的數值。
承諾協議 一個承諾協議方案由兩個算法構成:
● com:=commit(msg, nonce),承諾函數將信息(msg)和一個臨時隨機數(nonce)作為輸入,輸出就是一個「承諾」。
● verify(com, msg, nonce),驗證函數將某個承諾輸出(com)、臨時隨機數(nonce)及信息(msg)作為輸入,如果com==commit(msg, nonce),則返回「真」(true);反之則返回「假」(false)。
我們要求以下兩個安全特性要成立:
● 隱秘性:已知com,沒有可行的方法找到msg。
● 約束性:沒有可行的辦法找到兩組(msg, nonce)和(msg』, nonce』),msg≠msg』,而commit(msg, nonce)==commit(msg』, nonce』)。
為了使用承諾方案,我們首先需要產生一個臨時隨機數。然後將這個臨時隨機數與承諾信息msg一起代入承諾函數,計算承諾函數輸出值com,然後公佈該輸出。這個過程就如同將封好的信封放到一個人人能看到的桌上那樣。之後,如果我們希望展示之前的承諾值,我們首先公佈用於產生承諾的臨時隨機數,並公佈信息msg。此時任何人都可以驗證這時公佈的msg是否為之前承諾,這個階段就如同打開信封。
對於每次的承諾值,你都需要選擇新的隨機值,這一點很重要。在密碼學中,術語nonce是指,該取值只能使用一次。
以上兩個安全特性決定了這一算法就如同密封及打開信封。第一,如果僅僅知道com,即承諾函數的輸出,就如同只看信封並不能得到信息內容;第二就是約束性,這就保證了你一旦承諾信封內的內容,就不能再改變主意。也就是說,我們無法找到兩個不同的信息,當你在承諾一個信息後,而又聲稱你承諾了另一個信息。
我們如何在承諾協議中保證隱秘性和約束性這兩個性質成立呢?在討論這一點之前,我們需要討論如何執行承諾方案。我們可以通過使用加密的哈希函數來達到目的,考慮如下承諾協議實施方案:
commit(msg, nonce):=H(nonce∥msg)
其中,nonce為長度為256位的臨時隨機數。
為承諾一段消息,我們首先生成一個256位的臨時隨機數,然後將這個臨時隨機數與信息鏈接,並返回這個鏈接值的哈希值,來作為承諾輸出。為了便於驗證,我們還要設定其他人來計算一下臨時隨機數與信息鏈接之後的哈希值,比對一下計算結果是否與承諾輸出相同。
再來看一下我們的承諾方案要求的兩個特性,如果我們將承諾和驗證換成H(nonce∥msg),那麼這些特性就變成:
● 隱秘性:已知H(nonce∥msg),沒有可行方法找到msg。
● 約束性:沒有可行方法找到兩對(msg, nonce)和(msg』, nonce』),msg≠msg』,而H(nonce∥msg)==H(nonce』∥msg』)。
承諾的隱秘特性正是我們要求哈希函數要具備的隱秘性,如果將一個解密鑰匙選定為256位的隨機值,那麼由隱秘性得出,如果解密鑰匙與信息鏈接,那麼僅僅從哈希函數的輸出中恢復信息就是不可行的。約束性隱含在哈希函數的碰撞阻力特性中[3],如果哈希函數具有碰撞阻力,那麼我們將不能找到不同的msg及msg'值,而H(nonce∥msg)=H(nonce'∥msg'),如果這種情況發生,將構成碰撞。
因此,如果哈希函數H具有碰撞阻力及隱秘性,從安全特性上來講,這個承諾方案將有效。
特性3:謎題友好
哈希函數需要的第三個安全特性為謎題友好特性。這一特性較為複雜,我們首先解釋該特性的技術要求,然後通過舉例來闡釋該特性的意義。
直覺上,謎題友好可以這樣解釋,如果有一個人想找到y值所對應的輸入,假定在輸入集合中,有一部分是非常隨機的,那麼他將非常難以求得y值對應的輸入。
謎題友好 如果對於任意n位輸出值y,假定k選自高階最小熵分佈,如果無法找到一個可行的方法,在比2n小很多時間內找到x,保證H(k∥x)=y成立,那麼我們稱哈希函數H為謎題友好。
應用:搜索謎題
現在,讓我們試想一個應用以闡釋謎題友好特性的意義。在這個應用中,我們將建立一個搜索謎題,該謎題是一個需要對龐大空間進行搜索,才能找到解決辦法的數學問題。該搜索謎題沒有捷徑,也就是說除了搜索龐大的空間來進行求解,別無他法。
搜索謎題 搜索謎題構成:
● 一個哈希函數H。
● 從高階最小熵分佈選出的一個取值,id(我們稱其為謎題ID)。
● 目標集合Y。
該謎題的解決方法為一個解,x,應該滿足以下公式:
H(id∥x)∈Y
這個直覺是:如果H有一個n位輸出,那麼它的可能取值有2n個。解決這個謎題要求找到一個位於集合Y(通常比所有輸出值集合小很多)內的輸出值,Y的大小決定了謎題的難度。如果Y是所有n位字符串的集合,這個謎題就毫無意義。然而,如果Y只有一個元素,那麼這個謎題難度最大,謎題ID取自高階最小熵分佈,這個事實保證了求解無捷徑。反過來,如果該ID的確定性很高,那麼有人可能會作弊,比如通過使用該ID,事先對謎題進行求解。
如果一個哈希函數具備謎題友好特性,這就意味著對於這個謎題沒有一個解決策略,比只是隨機地嘗試x取值會更好。因此,如果我們要把謎題做成很難解決是可以的,只要我們能用適合的隨機方式生成謎題ID。當我們討論比特幣採礦(是一種搜索謎題)時會採用這一思路。
安全哈希算法
我們討論了哈希函數的三個特性及其相應的應用。現在,讓我們討論本書中將會大量用到的一個哈希函數,安全哈希算法(Secure Hash Algorithm 256,簡稱SHA-256)。哈希函數有很多,但SHA-256是一個主要被比特幣世界採用,並且效果還很不錯的哈希函數。
回想一下,我們要求哈希函數可以用於任意長度輸入。幸運的是,只要我們能建立一個用於固定長度輸入的哈希函數,然後通過一般方法,就可以將接受固定長度的哈希函數轉化為可接受任意長度輸入的哈希函數,我們稱這個轉換過程為MD(Merkle-Damgard)變換,SHA-256是採用這種變換方法的常用哈希函數之一。在通用術語中,這種基礎型,可用於固定長度,具備碰撞阻力的哈希函數被稱為是壓縮函數(compression function)。經過驗證,如果基本壓縮函數具有碰撞阻力的特性,那麼經過轉換而生成的哈希函數也具有碰撞阻力。
MD變換很簡單。比如壓縮函數代入長度為m的輸入值,並產生長度短一些為n的輸出值。哈希函數的輸入(可為任意大小)被分為長度為m-n的區塊。MD變換運作過程如下:將每個區塊與之前區塊的輸出一起代入壓縮函數,注意,輸入長度則變為(m-n)+n=m,也剛好就是壓縮函數的輸入長度。對於第一個區塊而言,之前沒有的區塊,我們需要選取一個初始向量(見圖1.3)。每次調用哈希函數,這個數字都會被再一次使用,而在實踐中,你可以直接在標準文檔中找到它。最後一個區塊的輸出也就是你返回的結果。
SHA-256函數利用了這樣的一個壓縮函數,這個壓縮函數把一個768位的輸入壓縮成一個256位的輸出,每一個區塊的大小是512位。我們可以通過圖1.3來理解SHA-256的工作過程。
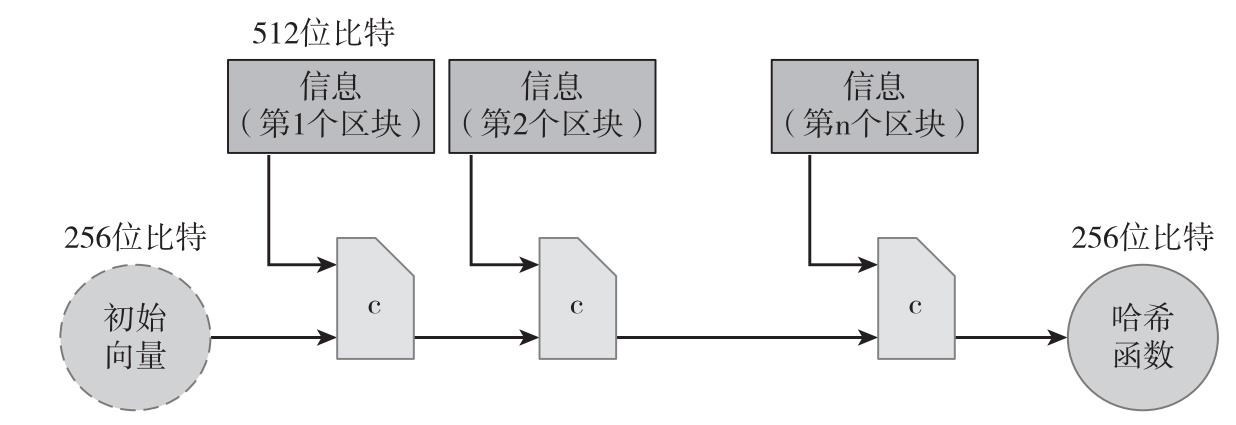
圖1.3 SHA-256哈希函數簡化圖
註:SHA-256利用MD變換把一個固定輸入的防止碰撞的壓縮函數變換成一個接受任意長度輸入的哈希函數。通過初始化向量的補位,可以把輸入變成512位比特的整數倍。
截至目前,我們已經討論了哈希函數、密碼學上使用具備特性的哈希函數、這些特性的應用,以及在比特幣世界中使用的一類特殊的哈希函數。在下面的章節中,我們將討論通過哈希函數來構建比特幣網絡中的更為複雜的數據結構。
 哈希函數建模
哈希函數建模
哈希函數是密碼學中的瑞士軍刀:它們在眾多各具特色的應用中找到了一席之地。這種多功能性的另一面是,為了保證安全,不同的應用會要求不同的哈希函數特性。事實已經證明,要確定一系列哈希函數特性以全面達成可證安全極度困難。
本書中,我們會選出在比特幣和其他加密數字貨幣中,對哈希函數使用方式很重要的三個特性。即使在這個範圍內,並非所有這些特性對哈希函數的每一次使用都有必要。比如,我們之後會看到,謎題友好只在比特幣採礦中具有重要性。
安全系統設計師常常會放棄,並且把哈希函數建立成對於任意一個可能的輸入,都會得到一個獨立的隨機輸出的函數。這種使用「隨機預言模式」來證明安全的做法在密碼學中仍具爭議。不論在這個辯論中你的立場如何,在建立安全系統時,當我們應用哈希函數基本特性,推論如何減少安全特性的數量,都是寶貴的智力訓練。本章的目的便是幫你學習這一項技能。
[1] 生日悖論是指,如果一個房間裡有23個或23個以上的人,那麼至少有兩個人的生日相同的概率要大於50%。這就意味著在一個典型的標準小學班級(30人)中,存在兩人生日相同的可能性更高。對於60或者更多的人,這種概率要大於99%。——譯者注
[2] 3和3+2256對2256求餘數之後,結果都是3。——譯者注
[3] 結論反之不成立,就是說,我們可以找到碰撞,但都不是滿足H(nonce∥msg)==H(nonce'∥ msg')意義下的碰撞。例如,你可以對於同一個信息來產生滿足同一承諾的隨機數,但這裡的哈希函數不具備碰撞阻力特性。
