本節將討論哈希指針(hash pointer)及其應用。哈希指針是一種數據結構,這種數據結構在我們即將討論的很多系統中都很有用。簡單來說,哈希指針是一個指向數據存儲位置及其位置數據的哈希值的指針。一個普通的指針可以告訴你數據存儲的位置,哈希指針不但可以告訴你數據存儲的位置,並且還可以給你一種方式,讓你驗證數據沒有被篡改過(見圖1.4)。
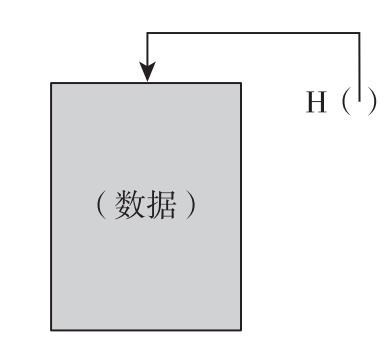
圖1.4 哈希指針
註:哈希指針是一個不但可以指向數據存儲的位置,還可以明晰某個時間戳下該數據的哈希值的指針。
我們可以利用哈希指針構建各種各樣的數據結構。為求直觀,我們可以把原來用普通指針實現的數據鏈表和二叉查找樹通過哈希指針來實現。
區塊鏈
如圖1.5所示,我們通過哈希指針構建一個鏈表,我們將這個數據結構稱為區塊鏈(block chain)。在普通鏈表中有一系列區塊,每個a區塊既有數據也有一個指向上一個區塊的指針。而在區塊鏈中,上一個區塊指針被置換為哈希指針。因此,每個區塊不僅能告訴我們上一個區塊的值在哪裡,還包含了該值的摘要,使我們能夠驗證那個值沒有改變。我們存儲鏈表頭部(the head of list),即一個普通的哈希指針指向最近使用的數據區塊。
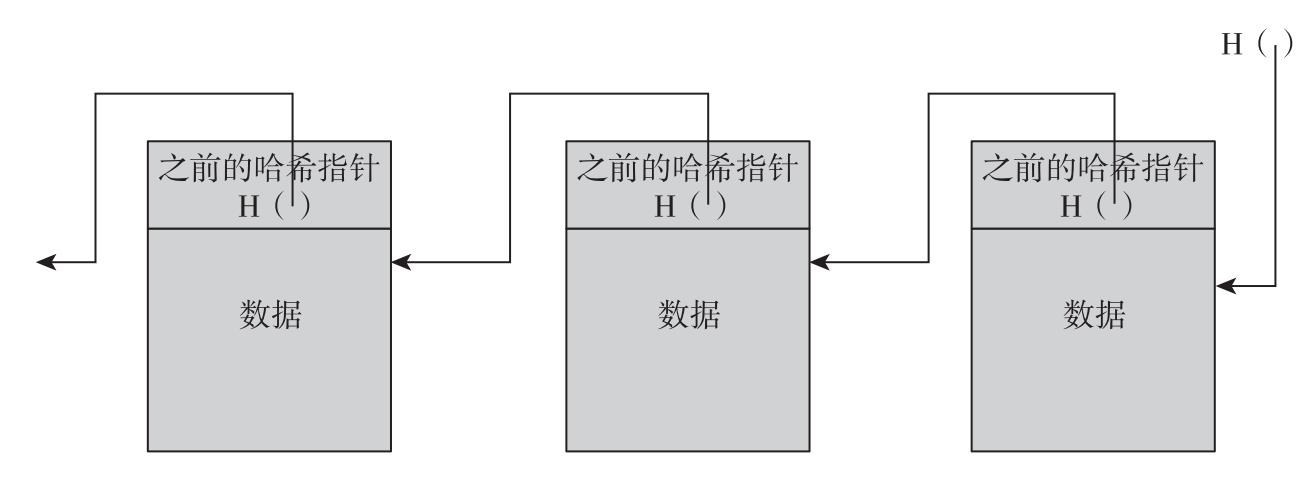
圖1.5 區塊鏈
註:通過哈希指針而不是普通指針構建的一個鏈表,我們把這個鏈表稱為區塊鏈。
區塊鏈的一個應用就是「防篡改日誌」。也就是說,我們要建立一個存儲很多數據的日誌數據結構,使我們能將數據附加到日誌的末尾。但是如果有人篡改日誌前面的數據,我們可以檢測到。
要理解區塊鏈如何實現這一防篡改特性,我們先看一下如果對手要篡改區塊鏈中間的數據會發生什麼。具體來說,通過這種方式,對手的目的是讓只記得區塊鏈頭部哈希指針的人無法檢測到篡改行為。為達到這個目標,對手會改變某區塊k的數據。既然數據已經被改變,區塊k+1的哈希值(即整個區塊k的哈希值)將不會匹配。記住,因為哈希函數具有碰撞阻力,我們可以確定新的哈希值與改變後的內容不會匹配。因此,我們會檢測到區塊k中的新數據以及區塊k+1中的哈希指針的不一致性。當然,對手可以繼續嘗試,並通過篡改下一個區塊的哈希值掩蓋這次篡改。他可以一直這樣做,但是當他到達鏈表的頭部時,這個策略將會失敗。具體來說,只要我們將鏈表頭部的哈希指針存儲在對手無法改動的地方,對手將不能做到在不被檢測到的前提下,篡改任何區塊(見圖1.6)。
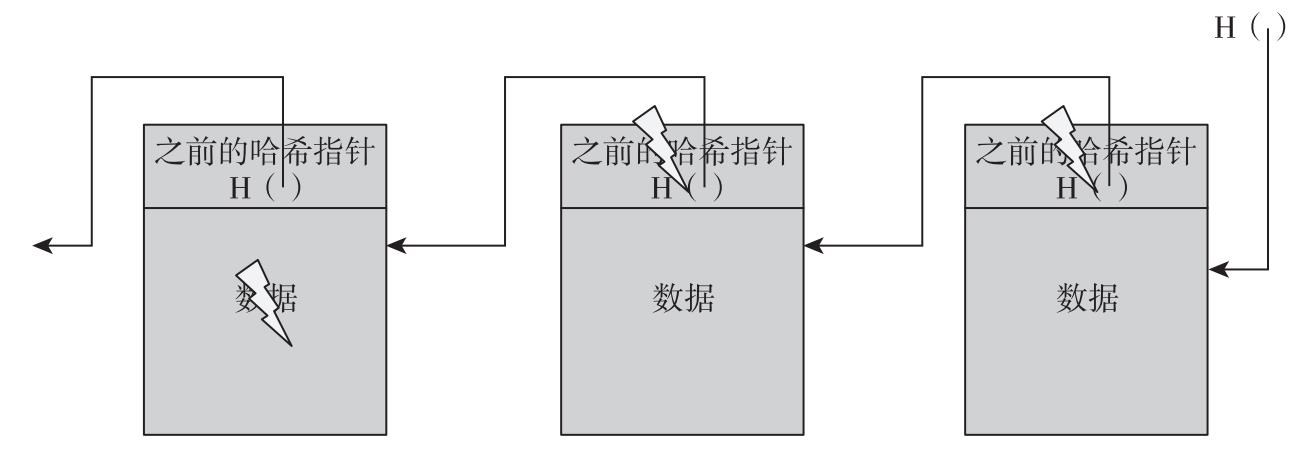
圖1.6 防篡改日誌
註:如果對手修改了區塊鏈中的任意部位的數據,那麼將會導致下一個數據塊的哈希指針不正確。如果我們鎖定區塊鏈的頭部數據,那麼即使對手修改了所有哈希指針使其與修改過的數據一致,那麼他也無法修改頭部數據,從而我們就可以檢測到篡改行為。
這樣做的結果是,如果對手想要篡改區塊鏈中任意地方的數據,為了保證整個內容一致,他需要篡改所有的哈希指針直至最開始的地方。他最終將碰到障礙,因為他不能篡改鏈表頭部的指針。這樣,我們便知道,僅通過記住一個哈希指針,我們就基本記住了整個鏈表的防篡改哈希值。因此,我們可以搭建一個包含很多區塊的區塊鏈網絡,鏈表頭部的哈希指針被稱作創世區塊(genesis block)。
你可能已經注意到了,區塊鏈的結構與我們上一節見到的MD變換類似。的確,它們很相似,同一個安全論證對於兩者都適用。
梅克爾樹
另一個我們可以用哈希指針建立的有用的數據結構是二叉樹。使用哈希指針的二叉樹也叫作梅克爾樹(Merkle trees),以其發明者拉爾夫·梅克爾(Ralph Merkle)的名字命名。如圖1.7所示,假設我們有很多包含數據的區塊,這些區塊就構成了樹的葉子(節點)。我們將這些數據區塊兩兩分組,然後為每一組建立一個有兩個哈希指針的數據結構,每個指針對應一個區塊,這些數據結構就構成了樹的下一個層次。我們輪流將這些區塊組兩兩分組,為每一組建立一個包含每個區塊組哈希指針的新的數據結構。以此類推,直到我們得到一個單一區塊,即樹根節點。
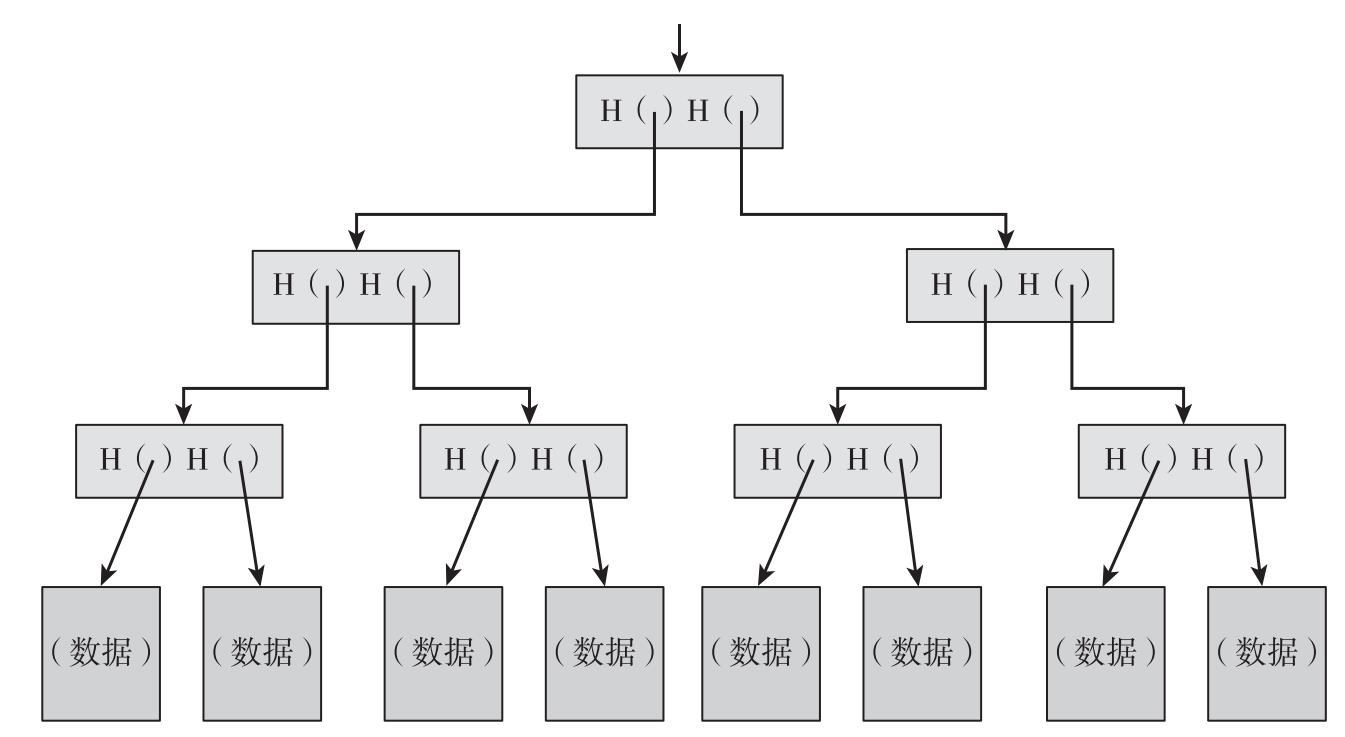
圖1.7 梅克爾樹
註:在梅克爾樹的數據結構中,所有的數據區塊都被兩兩分組,指向這些數據區塊的指針被存儲在上一層的父節點(parent node)中,而這些父節點再次被兩兩分組,並且指向父節點的指針被存儲在上一層的父節點中,一直持續這個過程,直到最後我們到達樹的根節點。
如上所述,我們要記住樹最前面的哈希指針。我們現在可以通過哈希指針回溯到列表中的任何位置,這讓我們能保證數據確實未經篡改,正如我們在區塊鏈見過的一樣,如果對手篡改了樹底部的一些數據區塊,會導致上一層的哈希指針不匹配,即使他繼續篡改這個區塊,改動數據行為將最終傳遞到樹的頂端,而此時,他將不能篡改我們存儲的哈希指針。因此,同樣地僅僅通過記住頂部的哈希指針,任何企圖篡改任何數據的行為都會被檢測到。
隸屬證明
與我們之前建立的區塊鏈不同,梅克爾樹的另一個特點是它可以實現簡潔的隸屬證明。假設某人想要證明某個數據區塊隸屬於梅克爾樹。同樣地,我們只記住樹根節點,然後他需要展示給我們數據塊信息,以及從該數據區塊通向樹根節點的那些區塊,我們可以忽略樹的其餘部分,這樣做是因為這些區塊已經足夠讓我們驗證通往樹根節點過程中所有的哈希值。其工作原理圖解參見圖1.8。
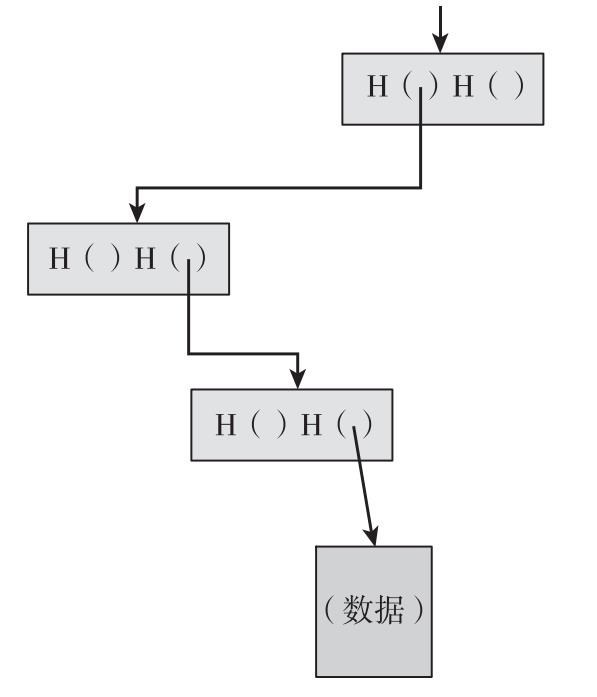
圖1.8 隸屬證明
註:為了證明某個數據區塊來自一個梅克爾樹,我們只需要找到該數據區塊到樹根節點的路徑。
如果整棵樹上有n個節點,只需要展示約log(n)個項目,因為每個步驟僅需要計算子區塊的哈希值,驗證過程需要時間約為log(n)。因此,即使梅克爾樹包含大量的區塊,我們仍可以在相對較短時間內證明隸屬關係。因此,驗證需要花的時間和涉及空間(樹節點)與log(n)同級。
一個排序梅克爾樹是把底層的數據通過某些排序得到的梅克爾樹,這裡排序規則可以是字母表排序、詞典排序、數字化排序,或者其他約定的排序方式。
非隸屬證明
有了排序梅克爾樹,我們可以在一個對數複雜度的條件下驗證某一個數據區塊並非來自某梅克爾樹。也就是說,我們可以證明某個特定區塊不屬於梅克爾樹,而我們只是簡單通過展示被驗證區塊之前的區塊路徑,以及被驗證區塊之後的區塊路徑,就可以達到目的。如果之前、之後兩個區塊在樹上是連續的,那麼這說明了被驗證區塊與該梅克爾樹之間是非隸屬關係。因為被驗證區塊確實隸屬於梅克爾樹,它需要在兩個條目之間,而如果兩個條目是連續的話,二者之間則並沒有空間。
我們討論過在鏈表及二叉樹中使用哈希指針,但更廣泛地說,我們可以在任何以指針為基礎的數據結構中使用哈希指針,條件是數據結構不存在循環。如果數據結構中存在循環,那麼我們將不能使所有哈希值得到匹配。想一下,在一個非循環的數據結構中,我們可以在靠近節點的地方開始,或者在沒有指針的數據區塊開始,計算其哈希值,然後從後往前進行計算。但是在一個有循環結構的網絡中,並沒有一個根節點,可以讓我們去追溯。
因此,試想另一個例子,我們可以建立一個哈希指針定向的非循環圖。
我們能夠在該圖中非常有效地驗證隸屬關係,同時也方便計算。這樣的哈希指針使用方式是一個常見技巧,在分佈數據結構中、在本章後面會討論到的算法中以及本書中都會反覆提到。
