在本節,我們將討論數字簽名(digital signatures)。數字簽名是密碼學中的第二個重要部分,該理論和哈希函數一起,為我們後面討論加密貨幣奠定基礎。數字簽名被認為是對紙上手寫簽名的數字模擬。我們對數字簽名有兩個特性要求,使其與我們對手寫簽名的預期一致。第一,只有你可以製作你自己的簽名,但任何看到它的人都可以驗證其有效性;第二,我們希望簽名只與某一特定文件發生聯繫,因此該簽名不能用於表明你同意或支持另一份不同的文件。對於手寫簽名來說,第二條就如同確保別人不能將你的簽名從一份文件上剪下來,貼到另一份文件的末尾那樣。
那我們如何通過密碼學來構建這些性質呢?首先,讓我們把之前的直觀討論說得更具體一些,以便今後可以更好地論證數字簽名方案,並討論其安全特性。
數字簽名方案
數字簽名方案由以下三個算法構成:
● (sk, pk) :=generateKeys(keysize) generateKeys方法把keysize作為輸入,來產生一對公鑰和私鑰。私鑰sk被安全保存,並用來簽名一段消息;公鑰pk是人人都可以找到的,拿到它,就可以用來驗證你的簽名。
● sig:=sign(sk, message) 簽名過程是把一段消息和私鑰作為一個輸入,對於消息輸出是簽名。
● isValid:=verify(pk, message, sig) 驗證過程是通過把一段消息和簽名消息與公鑰作為輸入,如果返回的結果是真,證明簽名屬實;如果返回的結果為假,證明簽名消息為假。
我們要求以下兩個性質有效:
● 有效簽名可以通過驗證,即:
verify(pk, message, sign(sk, message))==true
● 簽名不可偽造。
我們注意到generateKeys和sign都可以採用隨機算法。的確,generateKeys最好是隨機的,因為它需要為不同的人生成不同的密鑰,而verify則需要是確定的。
現在,讓我們更詳細地檢驗我們要求數字簽名方案具備的兩個特性。第一個特性很直接,那就是有效的簽名必須通過驗證。如果我用我的密鑰sk簽署了一條消息,之後有人試圖通過使用我的公鑰pk驗證關於同一條消息的簽名,該簽名必須證實為正確。這個特性是對簽名有效的最基本要求。
不可偽造性。第二個要求計算上不可能偽造簽名。也就是說,知道你公鑰並看到你在某些信息上簽名的對手,不能偽造他還未見過的你在其他信息上的簽名。這一不可偽造特性類似於我們與對手之間在進行一場遊戲,遊戲的使用在密碼安全證明中很常見。
在不可偽造性遊戲中,對手會聲稱他可以偽造簽名,而挑戰者會測試他所說的話(見圖1.9)。我們做的第一件事是使用generateKeys方法生成一個密鑰,以及相應的公共驗證公鑰,我們將密鑰交給挑戰者,然後將公鑰交給挑戰者以及對手。因此,對手只知道公共信息,而他的任務是試圖偽造一條信息。挑戰者知道密鑰,因此他可以簽名。
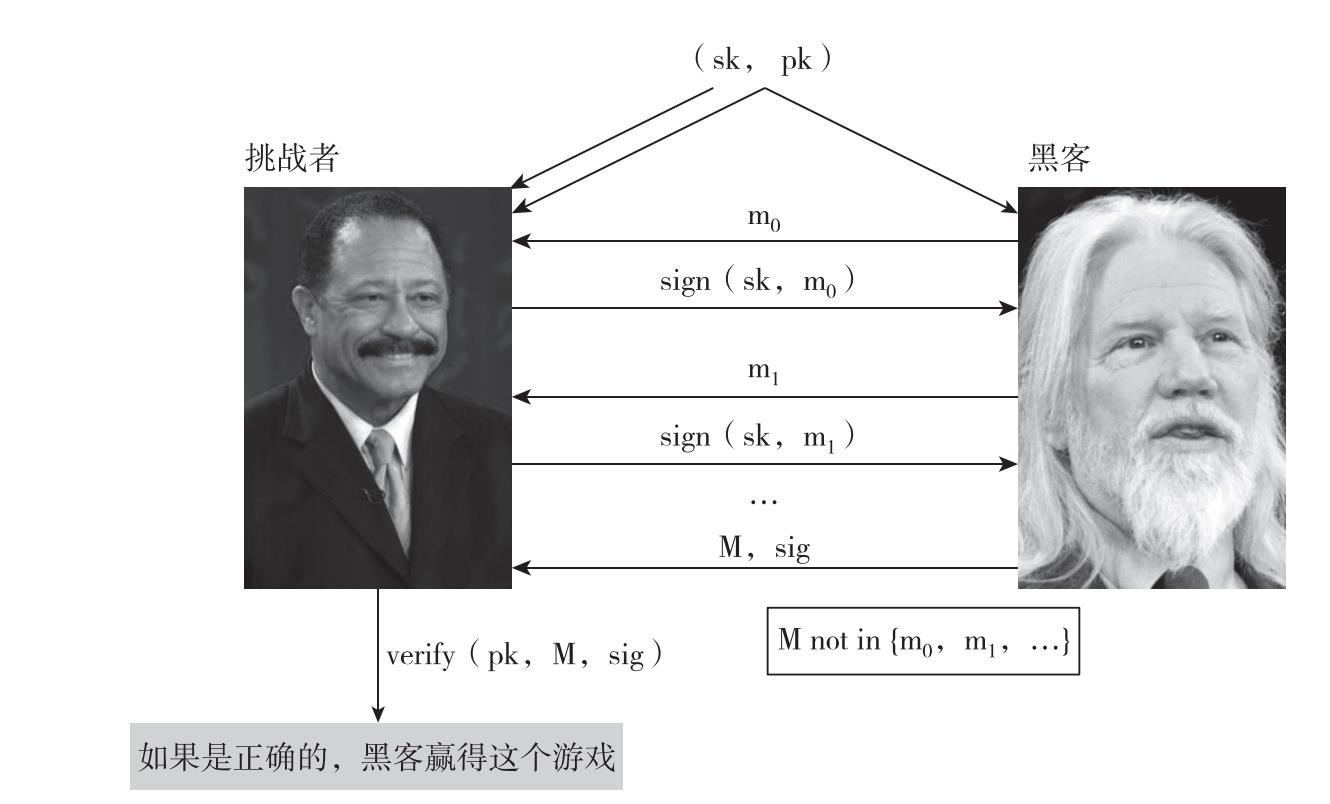
圖1.9 不可偽造性遊戲
註:不可偽造性遊戲是對手(黑客)和挑戰者一起玩這樣一個遊戲:如果黑客可以在一個之前沒有見過的消息上進行簽名,那麼黑客就贏得這個遊戲;反之,如果黑客做不到,挑戰者就贏得遊戲,從而可以證明這個數字簽名方案是不可偽造的。
直觀來看,這個遊戲的設定與真實世界條件一致,現實中的攻擊者很可能可以從潛在受害者的很多不同文件中看到有效簽名,攻擊者甚至還可能操控受害者簽署一份看起來無害但對黑客有利的文件。
為了將這一點建模到我們的遊戲中,我們將允許黑客選擇一些文件的簽名,不限時長,只要猜測的數量合情。合情猜測數量的意思是,我們允許攻擊者嘗試猜測的次數高達百萬,但數量高達280就不行了。從漸進性角度來說,我們允許攻擊者多次嘗試,嘗試次數可以是一個密鑰大小的多項式函數,但次數不能更多(例如攻擊者不能以指數方式猜測)。
一旦攻擊者滿意他所看到的簽名數量,那他就可以挑選某條信息M,嘗試在上面偽造簽名。對M的唯一限制就是,它必須為攻擊者之前未在之上看過簽名的信息(因為很明顯,攻擊者可以發出他收到過的簽名)。挑戰者運行驗證算法,以此確定攻擊者生成的關於M信息簽名在經過公共驗證密鑰驗證後,是否屬實。如果驗證成功,攻擊者贏得遊戲。
不論對手使用什麼算法,我們說籤名方案不可偽造,當且僅當他成功偽造信息的機會非常小——小到我們可以假設在實踐中從不會發生。
實踐中的考量
要將算法概念轉化為現實中可執行的數字簽名機制,我們還需要考慮許多實際問題。例如,很多簽名算法是隨機的(特別是比特幣使用的算法),因此我們需要隨機性的良好來源。我們不能低估這一點的重要性,因為不良隨機性會使你認為安全的算法變得不安全。
另一個實際問題是關於信息大小。在實踐中,你能夠簽署的信息大小是有限制的,因為真實的方案將在位數長度有所限制的字符串中運行。有一個簡單的方法可以解決這個限制:對信息的哈希值進行簽署,而非對信息本身進行簽署。如果我們使用輸出值為256位的加密的哈希函數,那麼我們可以有效地簽署任何長度的信息,只要我們的簽名方案能夠簽署256位的信息。如上所述,我們可以將信息的哈希值作為信息摘要,哈希函數具有碰撞阻力,因此這種方式是安全的。
我們後面會用到的另一個技巧是,可以對於哈希指針進行簽署。如果你簽署了哈希指針,那麼該簽名覆蓋(或者說保護)整個結構——這不僅僅是哈希指針本身,還包括哈希指針指向的整個區塊鏈。比如,如果簽署了區塊鏈末尾的哈希指針,其結果就是你有效地數字簽署了整條區塊鏈。
橢圓曲線數字簽名算法
現在讓我們來看一下具體的細節。比特幣使用的數字簽名方案叫作橢圓曲線數字簽名算法(ECDSA)。ECDSA為美國政府的標準,是早前DSA[1]算法利用了橢圓曲線的升級版。這些算法經過了數年的細緻密碼分析,且被普遍認為是安全的。
更具體地說,比特幣使用ECDSA算法,而不是標準橢圓曲線「secp256k1」[預計提供128位安全保障,即打破這個算法的難度與執行2128對稱性密鑰運算(如破解哈希函數)一樣困難]。雖然這個曲線是公開標準,但除比特幣以外鮮有使用,其他使用ECDSA的應用(如安全網絡瀏覽時的TLS[2]密鑰交換)通常都使用更常見的「secp256k1」曲線。這就是比特幣的一個古怪之處,因為在比特幣系統早期實施中被中本聰選定(參見原版前言),現在已很難改變。
我們不會詳細地討論ECDSA的原理,因為這涉及一些過於複雜的數學知識,且對於本書的其他內容沒有太多幫助。如果你對ECDSA感興趣,請參見本章末尾延伸閱讀部分。雖然我們這麼說,但對於瞭解各種參數也許會很有必要:
個人密鑰:256位
公鑰(未壓縮):512位
公鑰(壓縮):257位
待簽名信息:256位
簽名:512位
注意,嚴格來講,雖然ECDSA只能簽署256位的信息,但這存在問題,因為信息在簽署之前總是已經經過哈希壓縮,因此,任何大小的信息都能被有效簽署。
使用ECDSA時,確保隨機性良好來源至關重要,因為不良來源將可能導緻密鑰信息的洩露。這一點不難理解,如果你使用了不良隨機來生成密鑰,那麼該密鑰就可能不安全。但是ECDSA的古怪就在於,即使你僅僅只是在生成簽名時使用了不良隨機,而你使用的密鑰完美無缺,你的個人密鑰還是有可能洩露(熟悉DSA的人都知道這是DSA的古怪之處,但並不針對橢圓曲線)。接著遊戲就結束了,如果你的個人密鑰洩露,對手就可以偽造你的簽名。因此,我們在實踐中要特別注意使用良好隨機來源,使用不良隨機來源是安全系統的一個常見缺陷。
數字簽名作為密碼學基礎,我們對其討論就此結束。在下一節,我們將討論對打造加密貨幣會帶來幫助的一些數字簽名應用。
 加密貨幣及加密術
加密貨幣及加密術
如果你一直在期待比特幣使用的加密算法,我們可能會讓你失望了,比特幣並沒有使用任何加密術,因為並沒有加密的需要。加密術只是因為現代密碼學而變得可能成為眾多技術中的一個,很多技術(如承諾方案)在某種程度上隱藏信息,但是與加密術有所不同。
[1] DSA (Digital Signature Algorithm),電子簽名算法。——譯者注
[2] TLS(Transport Layer Security),傳輸層安全協議,用於在兩個通信應用程序之間提供保密性和數據完整性。——譯者注
