我們現在來討論一下如何在比特幣裡舉行一個「擲硬幣」的遊戲。首先看一下,在線下是如何建立這個系統的。
愛麗絲和鮑勃想要下一個5美元的賭注。他們在下注之前商量好了遊戲規則。鮑勃往空中扔一個硬幣,愛麗絲在硬幣落地之前叫出「正」或「反」面。當硬幣落地的時候,可以立即判斷誰是贏家。雙方都知道這個結果有足夠的隨機性,他們之中任何一人都沒有辦法影響結果。
為了使雙方相信這個遊戲是公平的,遊戲的步驟順序以及硬幣的特性至關重要。但上述設計有一個缺陷,就是他們二人都必須同時在場,而且相信對方會願賭服輸。在線上,我們也想設計一個同樣「公平」的博彩系統,同時確保輸家也會願賭服輸。
初看起來,這個應用有些古怪,並且有局限性,並不值得深入研究。非常有意思的是,一個基於比特幣的在線博彩系統中本聰之骰,已經被證明非常受歡迎,但它並未採用上述設計模式,而是依賴於某一方的信用,但它時不時地囊括了大部分比特幣網絡上的交易量。
我們想研究這種加密數字貨幣的「擲硬幣」系統的真正原因是,如果我們可以據此設計一個安全協議的話,也可以用這個技術來設計其他有趣和有用的協議。密碼學專家研究「多方參與的安全計算」,也就是說多個互相不信任的參與者,每個主體都有各自的數據,然後綜合各主體的數據來共同計算一個結果,但同時每個主體都不想讓其他參與者知道自己的數據是什麼。想像一個類似的場景,一次競價拍賣,但沒有一個可靠的拍賣行。通常這些計算需要被隨機化,來打破互相之間的關聯,最後,這個計算的結果是有金融屬性的,並且是不可逆轉的。比如,我們想要保證中標者最後會付款給拍賣物品的賣方,更進一步,讓賣方的(智能)資產自動轉移到中標者的名下,甚至更進一步,我們還想要懲罰那些不守規矩的人。
總而言之,一個安全的多方博彩系統雖然看起來簡單,但其實可以用來研究一個非常強大的系統模式:各自都有敏感數據的互不信任的一群參與者,共同來執行一個程序,不僅僅是為了控制數據,還可以控制與之關聯的資金。
在線擲硬幣系統
第一個挑戰是找到與「擲硬幣」相對應的線上的相關方法。假設我們有三個參與者:愛麗絲、鮑勃和卡羅爾,大家都想以相同的概率來選擇一個號碼1、2、3。我們嘗試以下協議:每個人選擇一個大的隨機數,比如愛麗絲選x、鮑勃選y、卡羅爾選z,然後互相告知各自的隨機數,並共同計算結果(x+y+z)%3。
如果他們都是完全獨立地選擇隨機數的話,這個方法是可行的。但請記住,這是在互聯網上,沒有辦法可以限制他們絕對地「同時」送出數據。愛麗絲可能會等到鮑勃和卡羅爾送出隨機數之後再發佈她的數據。這樣一來,她可以輕易地操縱這個計算的結果。我們沒有辦法設計出一個數據交換協議,它可以讓大家都相信沒有人會作弊。
為了解決這個問題,我們還是要回到函數約定。首先,每一個人選一個大的隨機數,並發佈它的哈希函數值;然後,每個人披露各自所選的數字;接著,其他兩個人查證這個被披露的函數值和在第一步發表的數據是否正確;最後,計算這個三個隨機數的結果,如下:
第一回合:
每個參與者選擇一個大的任意字符串。愛麗絲選x,鮑勃選y,卡羅爾選z。
每個參與者發佈對應的哈希函數值H(x)、H(y)、H(z)。
每個參與者驗證H(x)、H(y)、H(z)具有明顯的差異性(否則放棄這個協議)。
第二回合:
三個參與者分別披露他們所選的字符串x、y和z。
每個參與者查證這些字符串是否與第一回合裡發佈的函數值相吻合。
最後的輸出是(x+y+z)%3。
這種數據協議之所以能成功是因為以下因素:第一,因為函數的輸入x,y,z是大的任意數,沒有人可以在第一回合之後預測其他人的輸入;第二,如果愛麗絲按照規則任意地選擇她的輸入,她可以相信,不管鮑勃和卡羅爾是否選擇了隨機數,最後的輸出結果也是隨機的。
公平性
要是有人不披露約定怎麼辦?在這個協議的第二回合裡,假設卡羅爾一直等到愛麗絲和鮑勃披露他們的秘密隨機數,然後,在披露之前,意識到她會輸掉這一局,她就有可能拒絕公佈她的隨機數——她可以說她忘記了或是假裝下線。愛麗絲和鮑勃可能會懷疑,但他們也沒有什麼好的辦法去追查。
我們所要做的是立下一個規矩:參與者若是做出承諾,則必須在一定的時間內披露所選的隨機數。在密碼學裡,這個特性叫作公平性。比特幣提供了一個非常好的解決方法。
比如愛麗絲想要做出一個有時限的約定承諾,但鮑勃是唯一對此有顧慮的。第一,愛麗絲先設置一定的保證金,比特幣支出交易的腳本可以用來規定,這筆保證金只能用以下兩種支付情形:第一種支付情形是必須同時有愛麗絲和鮑勃兩人的共同簽名;第二種支付情形是只要愛麗絲披露了她的隨機數,以後消費這筆交易,就只需要有愛麗絲的簽名。如果愛麗絲所選擇的隨機字符串是x,那麼輸出腳本(ScriptPubkey)會包括哈希函數H(x)的值。
接下來,愛麗絲和鮑勃會同時簽下一個交易,把這個保證金支付給鮑勃(兩種情形之一)。但為什麼愛麗絲會同意這樣做呢?這個交易帶有一個nLockTime值來保障鮑勃不能在時間點t之前來贖取保證金。因為,在此時間之前,愛麗絲只要願意披露她的約定隨機值,她就可以贖回這個保證金,所以她的這個簽名交易是安全的。見圖9.5。
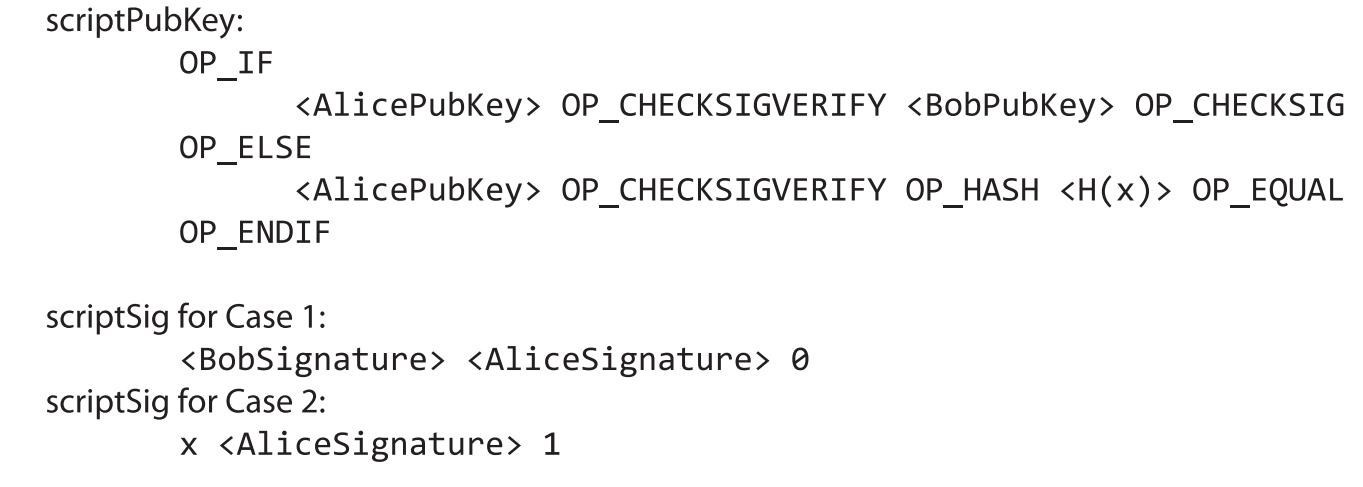
圖9.5 在有時限的哈希函數約定中使用輸出腳本和輸入腳本的交易輸出
如果愛麗絲在棄局之前沒有披露她的約定隨機數值,那麼鮑勃就可以在時間點t之後贖取該保證金。沒有人逼迫愛麗絲披露她的隨機數,但如果她不披露,她會因此失去預設的保證金。
我們如何用這個有時限的函數約定來實現安全的博彩系統?其實,架構和之前幾乎一樣,差別在於,我們不再採用簡單的函數約定,而是採用有時限的函數約定。任何一方,要贖回這筆保證金就必須把正確的隨機數值x披露出來;如果在最後期限到來時還不披露出他的隨機數值,就會放棄他的保證金,以用來補償其他兩個玩家。
可以在比特幣系統上實施這個博彩系統。但這個系統有些複雜,而且有時限的函數約定還要求多個非標準的交易。當系統裡有n個玩家的時候,由於每個玩家都要設置一筆保證金,我們需要n2個約定,此外玩家們還不得不投入比全部賭注更多的資金用來托管保證金。但對於參與者較少的遊戲來說,這是合理的,並且有更好的效率。最重要的是,這個遊戲驗證了本來認為不可能的數據交換協議,比如在線擲虛擬硬幣,並對不遵守規則的玩家進行懲罰,在比特幣的世界裡是可以做到的。
