在上一節,我們展示了一群人如何選擇一個公平的隨機數。在這一節裡,我們將討論如何用比特幣來產生一個對任何人都公平的公共隨機數。為什麼我們需要一個公共隨機數?讓我們先看一下幾個現實中已經存在的依賴公共隨機數的案例。
NBA新人選秀
其中一個例子就是每年春天的美國NBA聯賽的新人選秀大樂透。NBA聯盟中所有的30支球隊聚集在一起,根據上賽季每個球隊的賽季排名增加相應的權重,隨機選擇球隊選秀順序。在1985年,聯盟首次採取這種方法進行選秀,樂透選秀的過程通過電視現場直播,包含球隊名字的信封在一個透明的轉盤裡被充分打亂,委員會專員隨後去挑選這些信封。因為紐約尼克斯(Knicks)隊獲得了當年的狀元秀中鋒帕特裡克·尤因(Patrick Ewing),最終尤因也確實成為NBA名人堂的一員,當時這個樂透的產生引起了不小的爭議。由於那次的樂透發生在紐約,其他球隊的球迷宣稱整個過程被人操縱,並偏向尼克斯隊。
有很多有關NBA是如何操縱選秀過程的陰謀論,比如著名的「折角」論(「bent corner」 theory)是說包含有尼克斯的信封有一個角被故意折彎了,這樣委員會專員通過觸摸就可以分辨出哪個信封是尼克斯的。另外一個論調是說尼克斯的信封之前被放在了冷凍室裡,這樣專員可以通過選擇一個手感比較冷的信封來挑選出尼克斯隊。這些論調都反映了一個事實,這種類型的選擇要做到絕對公平是非常困難的,有很多合乎推理的作弊空間,想像一下一個職業魔術師的巧手可以做些什麼!直到今天,選秀樂透每年都會舉行,但每一次都充斥著各種陰謀論和謠言,以說明選秀並不是絕對公平的。
美國軍隊選秀
另一個更加嚴肅的案例是1969年的美國徵兵選秀,用於決定哪些年輕人會去參軍,大部分被選中的人事後都被派去參加了越南戰爭。同樣使用了一個類似於NBA選秀的方法,由美國國會派出的代表來主持選秀並通過電視直播(如圖9.6)。他們在一個大的塑料桶中放了很多小球,每個小球包含了一個數字,然後輪流從桶中把這些數字小球取出來,根據數字所代表的生日來決定優先級,根據這個優先級挑選合格的年輕人參軍。

圖9.6 1969年(越戰)軍隊選秀
1969年的這次徵兵選秀,是首次在全國範圍內採用樂透方式進行選秀。其目的是通過避開數以千計的本地徵兵委員會,以使選拔過程更加公平,並且向公眾公開這個過程。但遺憾的是,這個選秀樂透也演砸了,不到一個星期,概率專家通過數據調查分析注意到了一個特別的模式(如圖9.7所示):出生於下半年的人被選中的優先級較低。雖然這種差異非常細微,但是從概率統計上是非常顯著的,說明這不太可能是偶然事件。當他們回看現場錄像的時候,發現每次轉動轉盤的次數恰恰都是偶數次,這意味著一開始是上層的小球有較大的概率一直留在上層,說明為了形成隨機抽籤的混合程序並不充分。
這兩個案例都證明了,設計一個公眾認可的隨機過程並由此產生一個認可的公共隨機數,是十分困難的。無論你採用什麼方法,總有人懷疑你作弊。風險在於:這個隨機過程可能會被操作——即便這個過程是真正隨機的,但公眾並不信任它。[1]
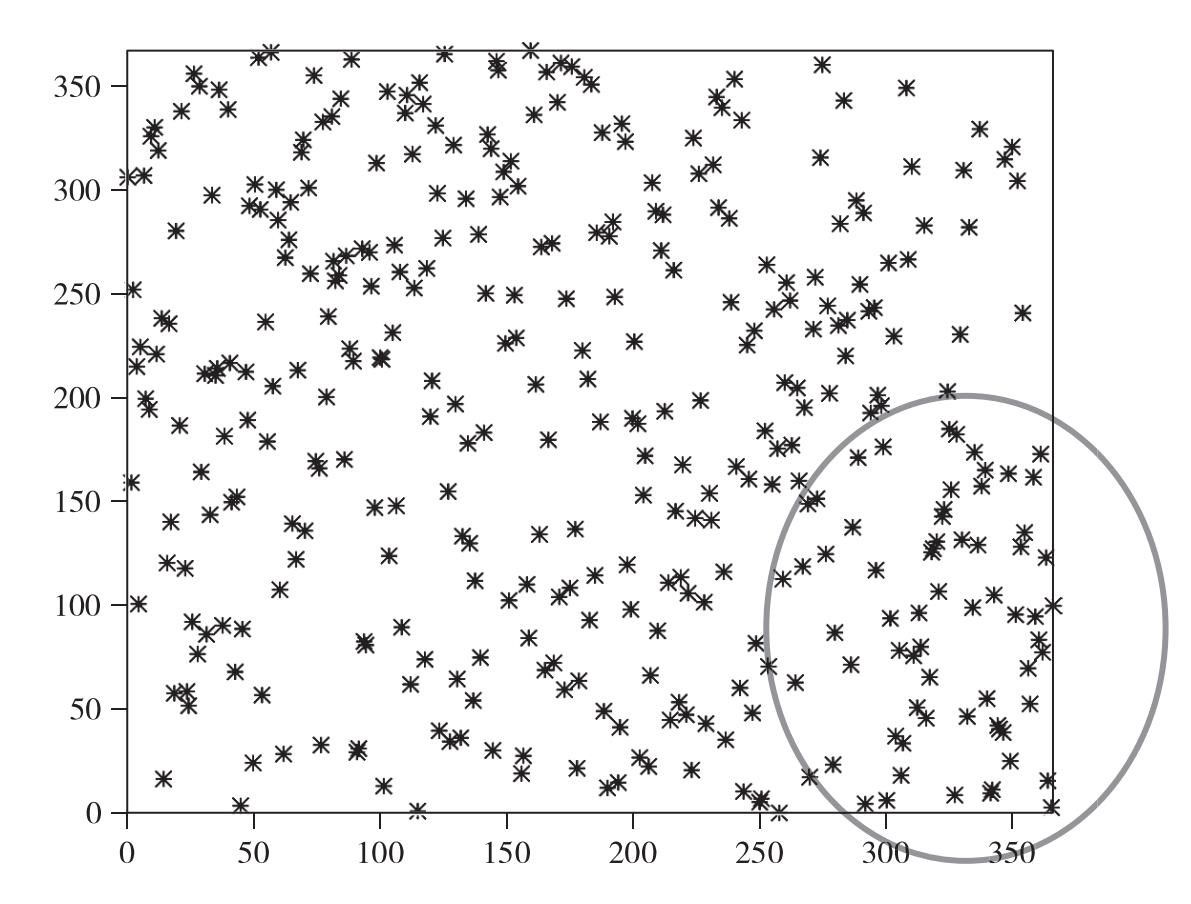
圖9.7 1969年徵兵選秀的概率統計偏差
註:x軸代表日期,y軸代表選秀號碼。
密碼學「信號塔」
由於成本低,並且大眾易於理解,用轉盤、拋硬幣、擲骰子等方法去展示公開隨機性,在歷史上一直比較普遍。但是這些方法非常難以審計,因此並不適用於大範圍的場景。即使整個過程從視頻上看起來是合法的,人們也有理由去懷疑樂透的執行者可以使用「魔術師之手」去操縱結果。
那麼,通過密碼學的辦法,我們是否可以做得更好?這裡,我們用密碼學「信號塔」(cryptographic beacons)來特指一個提供公共隨機源的服務。我們的想法是「信號塔」會源源不斷地在一個固定的頻率產生隨機數,並且沒有人可以預測這些隨機數。只要大家同意這一點——沒人可以預測這個信號塔的下一個輸出,那麼大家就都可以相信其生成的是一個真正的隨機數。
一個完美的密碼學信號塔可以服務於各種公開樂透項目,比如上面兩個例子。如果你想要在本地的俱樂部玩一個賓果(Bingo)遊戲[2],你再也不需要用一個大的轉盤來產生隨機性了。只要每個人都信任信號塔,就不要用物理的方法來展示隨機性了,這會省去很多麻煩。
密碼學專家提出了很多其他的公共隨機源的應用方案,包括投票系統、零知識驗證、分割選擇協議等。如果你有一個完美的密碼學信號塔,其中很多方案都會變得非常簡單有效。但遺憾的是,截至目前,我們還沒有找到一個完美的方案去打造這樣一個信號塔。
NIST信號塔
NIST,即美國國家標準與技術研究所(National Institute of Standard and Technology)。從2011年開始,NIST運行了一個它們自己的信號塔服務。它們聲稱用了一個非常複雜的實驗室裝置來產生隨機數,甚至動用了兩個糾纏態光子。由於隨機數是由量子力學現象產生的,那麼理論上這個數字可以保證非常強的隨機性。如果你認可海森堡不確定性原理(Heisenberg uncertainty principle)和其他一些被廣泛接受的物理學原理,那麼你就會相信這個信號塔產生的數是真正隨機的,並且不可預測。NIST信號塔服務可以每60秒產生一個附帶有數據簽名的隨機數,並提供一個非常便利的程序接口——服務可以通過網頁來訪問並返回隨機數。
從某種意義上說,NIST信號塔代表了從物理上展示隨機性的極限,但無法解決一個基本的信任問題——你必須信任NIST確實是通過它們所宣稱的這些程序來產生隨機數的,你必須信任在馬里蘭州的某一個建築裡面,NIST確實用它們的實驗室來產生這些隨機數,而不是偽造的,你還必須信任它們確實沒有能力故意重寫其中一些隨機數。
打造一個信號塔的其他潛在方法:自然現象
我們是否可以使用一些每個人都可以觀測到的自然現象來實現信號塔?或者我們可以使用天氣的一些細節,比如在某天某個特定地點的溫度,或者是風力的強度,或者是否會下雨。當然,我們有能力去提前預測天氣,但是預測的結果並不是非常精確,所以我們可以使用這些測量值的「最低有效位」。但是這個方法也有局限性,那就是需要所有的參與者在同一個地點做同樣的測量。
為了避免這個問題,我們可以利用太陽黑子,一種太陽表面的爆發活動(見圖9.8)。另外一個例子是宇宙背景輻射,通過廣播天線,你可以從地球上的任意一點都可以監測到這個數據,而且每個人都可以讀取到同樣的數值。這些都是超大範圍發生的現象,很容易向公眾證明沒有其他人可以操縱這個過程。想像一下,某人穿越宇宙到達太陽表面,然後用某種辦法去影響太陽黑子現象,而其目的僅僅是為了操縱地球上的某個樂透項目,這顯然是不現實的。所以上述這些方法都有很好的特性:公眾可觀測性、可防止被操縱性,以及一個可接受的不可預測性。

圖9.8 NASA太陽黑子照片
但上述這些方法都有一個共同的問題,就是生成隨機數太慢了。例如,如果隨機信號是當日最高溫度,那麼你每天只能獲取一次這樣的數值;太陽表面也不是經常變化,在很多密碼學應用中,隨機數通常作為偽隨機數發生器(Pseudo-Random Generator,簡稱PRG)的輸入,從安全角度考慮,這些輸入通常需要達到80比特位長度,甚至更多,但如果以天氣或者天文學為數據源,那我們可能需要很長時間才能積累到80位長度的隨機數。
另外,觀測太陽黑子現象這種方法還需要專業技能,所以你還需要依賴一些可信任的專業觀測者來獲取這些測量數據。由於有很多這樣的可信任的觀測者,我們也希望他們「互相之間有誠信」。信號塔的應用者,或者說是這些應用的用戶,可以隨時選擇並替換觀測者。這個特性被稱為「信任的敏捷性」,相比於NIST是提供信號塔服務的單一機構,這個特性更加優越。
還有更深層次的問題,雖然這個問題看起來可能微不足道,那就是,我們是否可以找到一個方法,它可以使一個現實世界的觀測數據——例如溫度、太陽黑子圖——轉變為一個數據字符串,並且它還需要保證每一個觀測者都獲得相同的字符串?我們可以嘗試數字化這個觀測數據:比如,我們用華氏度來描述溫度,並使用第一個十進制數位作為信號塔的輸出,但是除非每一個觀測者的溫度計都是不可思議的精準,否則就會出現下面的情形,有些觀測者讀取的溫度(比如)是62.7,而另外一些人讀取的則是62.8。目前看來,不管我們選擇哪種自然現象或者採用哪種協議,我們都會遇到這種「極端情況」。對於一個密碼學信號塔,即使測量值出現非連續性的可能性非常小,那也是無法接受的,因為這有可能使得PRG產生的隨機數變得完全不同。
金融數據
還有一個類似的想法是使用金融數據作為數據源,比如股票市場價格指數。同樣,這些是公開的可觀測的數值,而不像自然現象,這些金融數據本身就是用數字來呈現的,所以不會因為觀測者不同,產生數據不一致的問題;同時,我們有很好的理由相信,股票價格的小波動是很難預測的:如果你可以預測紐約證交所某一隻股票的交易價格,並且精確到美分級別,你就會成為一個非常賺錢的日內交易員。某些人可以通過買賣股票,去操縱股票價格到某一個特定的數值,但這需要巨大的成本。
但是,這種方法也需要依賴某一個信任方,比如股票交易所。即使股票交易所本身有很強的意願去建立自己的誠信,但如果讓它們操縱一個非常有利可圖的樂透,那麼它們就有可能去嘗試改變股票價格(例如,通過插入自己的買賣單)。
截至目前討論的方法,似乎很難去規避信任方的問題,而這個信任方卻是可以在整個過程中的某些關鍵環節對結果施加重要影響的。
用比特幣作為一個「信號塔」
幸運的是,把中央權威從數據交換協議中剝離出來,在之前認為幾乎是不可能的任務,而比特幣是很有希望實現這一任務的技術,而這也是本書的中心思想之一。我們是否可以把比特幣作為一個生成隨機數的「信號塔」呢?我們想要從比特幣的區塊鏈裡摘取隨機數,與此同時保留比特幣所有去中心化的特點,正是這些特點使比特幣如此吸引人。
我們回憶一下,礦工必須計算大量的隨機哈希函數來找到一個有效區塊。或許這意味著沒有人可以不經過挖礦工作就能預測或是影響下一個區塊的生成。當然,任何一個區塊的哈希函數結果的最初幾個字節都是零,但是在合適的假設下,唯一可以預測剩餘位數的比特值的方法可能是找到一個勝出有效區塊,然後選擇性丟棄它(見圖9.9)。
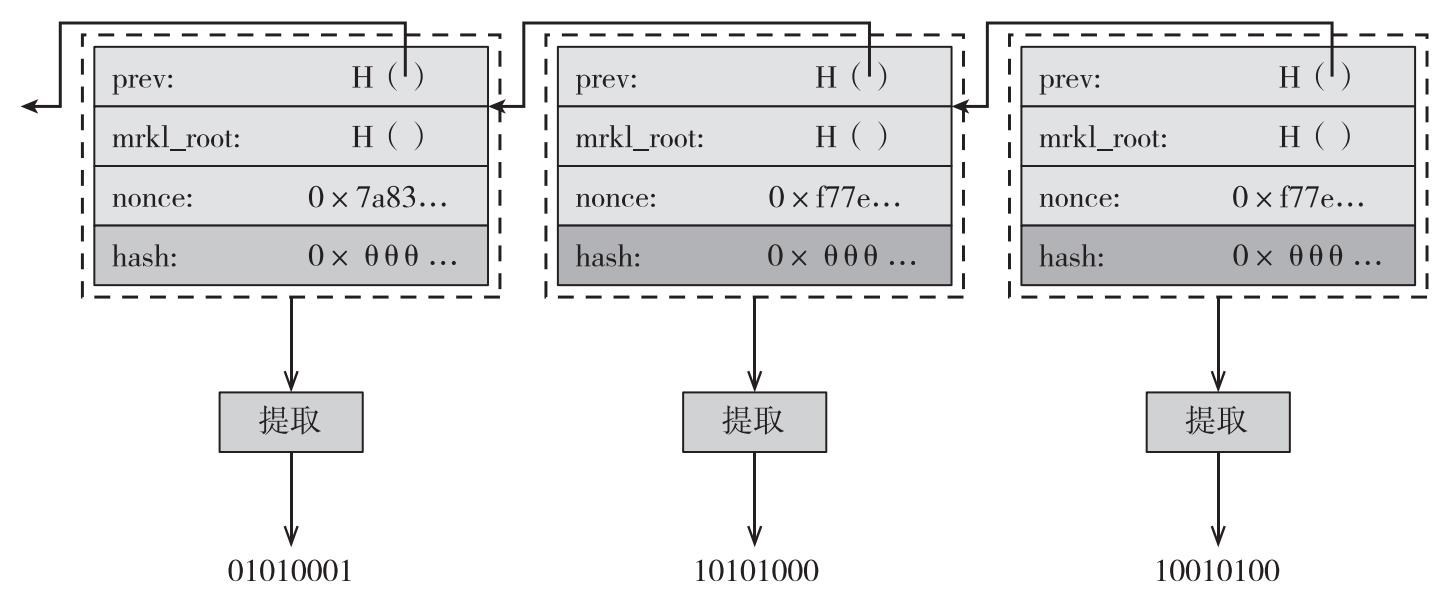
圖9.9 比特幣像燈塔一般
註:我們可以通過使用隨機提取功能,提取公共隨機數據,標注區塊鏈上的各個區塊。
這樣一來,把區塊鏈變成一個隨機數「信號塔」成了一件簡單的事。在區塊鏈上的每一個區塊上,我們在區塊頭部設置一個「隨機數抽取器」。隨機數抽取器,其實就是一個哈希函數,這個哈希函數把所有的輸入隨機熵均勻地壓縮成一個隨機字符串。每次只要發表一個區塊,我們就有了一個新的隨機信號輸出。
評估比特幣「信號塔」的安全性
假設你參加一個樂透抽獎,這個抽獎的結果是由未來將要產生的、一個預先設定的、位於高度h的某個區塊的輸出所決定的。這個樂透抽獎有N個參與者,每個參與者都下注了B個比特幣,如果你也是一名礦工,我們再假設,你幸運地找到了一個區塊h的函數解謎的答案,你就可以選擇發表或是不發表這一區塊。如果你不喜歡從這個區塊裡產生的抽獎的結果,你可以輕易地丟棄這一區塊,然後讓其他找到這個區塊的人來決定這個抽獎結果,但同時,你必須放棄因為找到這個區塊所帶來的收入。
讓我們計算一下,下注的數額B值需要多大,才值得考慮放棄區塊本身的獎勵。如果你成功地找到了一個位於高度h的區塊來決定抽獎的結果,然後意識到,如果你發表了這個結果,你肯定會輸掉抽獎;如果你扔掉這塊,你還是有1/N的概率來贏得B×N比特幣,這就意味著,如果你期望的抽獎獎勵(1/N)×B×N比特幣比挖礦所獲得的25個比特幣獎勵要大的話,那麼放棄區塊獎勵是合理的(在2015年,如果不考慮交易費的話,區塊獎勵大概是25個比特幣),所以如果B大於25,這種丟棄策略就是有利可圖的。在2015年中旬,25個比特幣價值大約在5 000美元左右。所以如果每個玩家下注不到5 000美元的話,並且假設每個玩家都是理智的,那麼這個樂透抽獎是可以抵抗放棄有效區塊這種攻擊的。
另一大優點是這是一個完全去中心化的信號源,沒有一個中心化的信託方。比起其他幾個信號源的方案,它的處理速度相當快,大概每10分鐘就產生一個輸出。然後通過上述的簡單模型,我們可以估計一個攻擊者想要操縱信號源輸出所需要付出的代價。
用比特幣作為信號塔辦法的一個缺點是,不能精確定時。比如,假設我們想要在明天正午讀取這個信號源的值,但我們無法知道哪個區塊在哪個時點會生成最新的一個區塊。雖然平均來說,在正午之前或之後的10分鐘內一定會有一個區塊被公佈,但這還是會有誤差。如果我們想降低目標區塊在一個短分叉事件中丟失的可能性,我們還要對有可能發生的延遲有所準備。在比特幣世界裡,通常情況下要等6個區塊(60分鐘)後,才能確信這個信號值是真正地被確認了。
另一個缺陷是,相對來說,操縱這個信號值所需的代價可能還是太低。如果我們用這個方法來實行NBA選秀,由於其中可能涉及幾千萬美元利益,球隊頓時就有了賄賂礦工來操縱選秀過程的動力。所以,當涉及巨額資金時,這個方法是否有效仍值得探討。
最後,我們的安全評估忽略了一些現實生活中的因素。比如,對於加入某一個礦池的礦工來說,丟棄一個有效區塊並不會讓他損失很多錢,因為他們是根據貢獻算力的比例,而不是區塊來領取獎勵的。所以,比特幣信號塔目前還是一個有趣但沒有被證明的想法。
腳本語言對信號塔的支持
如果我們擴展比特幣的腳本語言功能,加入一個特殊的操作碼(opcode)來讀取比特幣信號呢?按照最初的設計,現在的比特幣腳本語言沒有任何辦法去實現任何隨機性,因為礦工必須驗證腳本,而且一個腳本的有效性需要獲得所有礦工的認可,但如果我們用了信號塔產生的隨機數,由於這是一個可被證明的公共隨機數,把這個隨機數加入交易腳本中,礦工就容易隨機性地達成共識。
假設我們有一個操作碼可以做一個隨機的決定,這個決定是基於上個區塊的信號塔輸出的。我們可以把整個複雜的抽獎數據協議用一個腳本來替代——讀信號塔的隨機數值,然後把該輸出分派到n個密鑰中的一個。這需要有多回合的數據協議安全保證或是有時效的函數約定。
這個想法的一個缺點是,為礦工操縱抽獎提供了可能性,如果他們發覺挖到的這一個區塊裡的交易會讓他們輸掉這個抽獎,他們就會簡單地將抽獎交易延遲至後面的一塊出現。但是我們可以對信號塔的操作碼做一個小小的調整來防禦這類攻擊,也就是說,你不是用上一個區塊,而是使用某一個特定高度的區塊所產生的信號塔隨機數。
[1] 所以一個公平的不受操縱的公共隨機源是一個公共福祉,而比特幣可以做到這一點,因為它是去中心化的。——譯者注
[2] Bingo是一種填寫格子的遊戲,在遊戲中第一個成功者以喊「Bingo」表示取勝而得名。——譯者注
