下面是從一副撲克牌中隨機抽出的4張,每張牌都是一面寫有字母,另一面寫有數字。請決定你將翻動4張牌中的哪一張,以發現其是否符合下述原則:「如果一張牌的一面是元音字母,則其另一面為偶數。」只翻動必要的牌以確定此原則是否存在。你可以這樣記錄:如果你在電子閱讀器上閱讀,可以將你的選擇標黃;如果你閱讀的是紙質書,用鉛筆標出你的選擇。

我必須翻動的是:
a.只翻動牌3
b.翻動牌1、2、3、4
c.翻動牌3和牌4
d.翻動牌1、3、4
e.翻動牌1、3
我們隨後會將這個問題置於另一種情境中。
批判性推理的文本中往往充滿了形式和演繹邏輯。之所以會如此,主要是因為古代的教育傳統使然,而與今天的實用性思維不同。實際上,你大可以懷疑在本章中讀到的有關形式邏輯的內容在日常生活中的實用價值極其有限。
但是不可否認,仍有一些不錯的理由告訴你應當瞭解一些形式邏輯的知識。
1.對於科學與數學而言,形式邏輯是必要的。
2.本章展示了西方的有限理性與東方的辯證思想之間存在的明顯分異。這兩種思想體系可以應用於相同的問題上,但會得到截然不同的結論。將這兩種體系並置是一種很好的機會,我們可以借此找到兩者的缺陷。
3.一個受過教育的人應當對一些基本的形式邏輯形式進行學習。
4.至少對大多數人而言,形式邏輯充滿趣味性。(至少,也和這一章的體量一樣大!)
在西方,形式邏輯的起源大致是這樣的:亞里士多德厭倦了在市場和集會上聽到的那些糟糕的論斷。於是他決定發展出新的推理模式以便讓這種思維過程變得有效度。一個論點有效,當(且僅當)它的結論是從前提推斷出的。有效性與真實無關。當一個論點的敘述結構是恰當的時候,它就是有效的,而同時其結論可能是錯誤的。
論點有效性的概念是極其重要的,這有許多原因。第一,因為你不想讓別人欺騙你(或是自欺欺人),而他們欺騙的方式是告訴你某一個結論是合理的,而只因為此結論是從某個前提推斷出來的——除非那些前提是真實的,而結論是必然由其推出的。第二,我們不希望對自己不喜歡的結論質疑,而這些結論和推出它們的前提一樣恰巧都是真實的。第三,如果我們能對有效性和真實性的概念有清晰的理解,那麼我們就能拋開前提和結論的意義而單純地評估兩者之間的關係,即以純粹抽像的形式思考個中邏輯,就像可以把具體的鳥類和蜜蜂抽像成A群和B群。這樣的抽像思考能向我們揭示結論是如何從前提推出的,即便結論高度難以置信,但它至少並非是不合邏輯的推理結果。
三段論
亞里士多德對形式邏輯領域的一個重要貢獻是三段論。各式三段論在中世紀時勢如破竹般進入了家庭手工業領域,當時的僧侶們創造了許多。從中世紀到19世紀晚期,哲學家和教育學家都相信三段論為人類的思維提供了許多有力的規則。因此,他們在西方的高等教育課程中設置了大量相關學術訓練。
有關有效性的論題源自三段論,而這與分類推理有關。有些類型的分類推理包含了諸如「所有」「一些」「絕無」之類的數量詞。最簡單的三段論包含了兩個前提和一個結論。那些簡單的三段論中的最為簡單的一個,且我們通常不會弄錯的是:所有A都是B,所有B都是C,那麼所有A都是C。典型的表述如下:
所有職員都是人。
所有人都有兩隻腳。
所有職員都有兩隻腳。
這個論斷是有效的,因為結論是按照邏輯從前提中推出的。結論同樣是真實的。
所有職員都是人。
所有人都有羽毛。
所有職員都有羽毛。
這個論斷同樣是有效的,儘管結論是不真實的。但是結論的不合理會讓我們覺得這個論斷同樣是無效的。以A、B、C來替換職員、人和羽毛可以讓我們來看清楚這個論斷的有效性。這可能會強迫我們重新思考一個結論的真實性,而這一點十分重要。
下述論斷是無效的,即便其前提和結論都是真實的(或至少是高度可信的)。
所有接受救濟的人都貧窮。
一些窮人是不誠實的。
因此,一些接受救濟的人是不誠實的。
轉換成抽像形式即是:
所有A都是B。
一些B是C。
因此,一些A為C。
這種抽像化的練習十分有用,因為我們可能會覺得一些結論看似合理就認為它為真,並且以為我們在真實的前提下邏輯自洽地推斷出來的結論為真。發現一個論斷是無效的可以讓我們不再認為一個結論必然為真,並開始對其質疑。(辨識上述論斷無效性的關鍵在於,認識到A是B的一個子集。)
事情從這裡開始會迅速變得複雜起來:所有A為B,一些C是A,則一些C是B。有效嗎?沒有A是B,一些C是B,則沒有A是C。有效嗎?
你可以就這樣消磨時間,直到牛兒們都回家了。中世紀的僧侶就是在無聊打發時光的過程中想出了大量的三段論。然而,我同意哲學家伯特蘭·羅素的看法,這些三段論就像那些僧侶一樣枯燥無味。同樣的,2600多年來圍繞三段論而進行的教育對於有效思維也是無所裨益的。
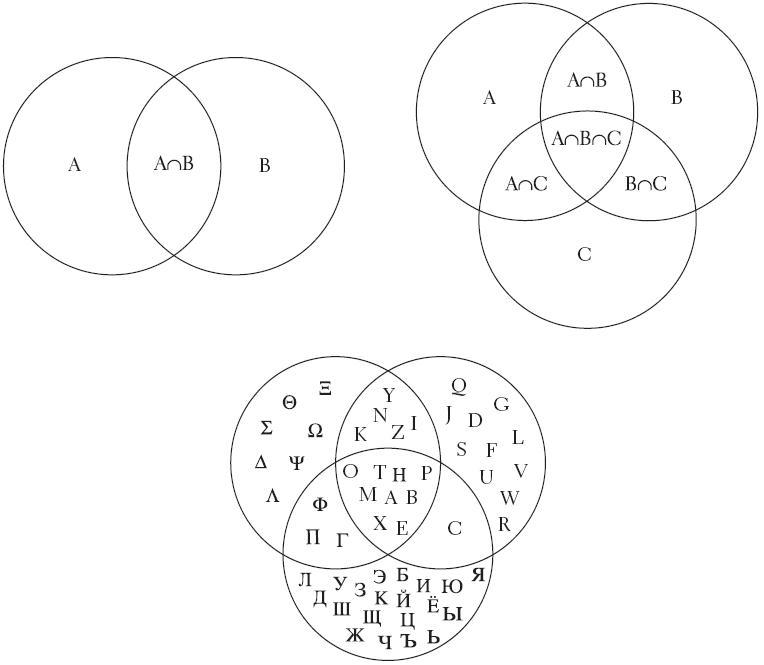
相互重疊的不同類別產生了交集
在我看來,能從分類推理中獲得的最有用的東西是學會如何畫文氏圖。此圖得名於19世紀的英國邏輯學家約翰·維恩,而維恩發明了一種繪圖方法,可以表現類別之間的關係。我常常會發現文氏圖很有用,甚至在有時候是表現類別之間關係的必要方式。上圖就展示了一些比較有用的文氏圖,讀者們可以感受一下。
在上圖中,左上角的圖形展示了一種我們日常生活中會用到的三段論。它展示的情形是:一些(但並非全部的)A是B,而一些(但並非全部的)B是A。A可能代表了小型有毛髮的動物,而B可能代表了鴨嘴恐龍。有一種動物剛好在A與B的交集上,那便是鴨嘴獸。或者我們也可以用左上角的圖來表示:在國際學校裡說英語的學生中有一部分同時會說法語,而說法語的學生中的一部分也說英語。(A中的一部分為B,而B中的一部分為A。)只說英語的學生(僅僅是A)必須跟史密斯太太學數學,只說法語的學生(B)必須跟著皮羅特先生學習。而說兩種語言的學生則可以跟兩位老師中的任意一位學習。
右上角的圖展示了一種更為複雜但也並不少見的情況:一些A為B,一些B為A,一些A為C,一些C為A,一些B為C,而一些C為B。
最下方的圖展示了上述情況的一個現實案例。它展示了希臘字母(左上圓圈)、拉丁字母(右上圓圈)和俄語字母(下方圓圈)的交集。我不相信你能僅僅通過口頭表達就弄清楚這些類別重疊的情況。無論如何,我覺得我只能借助字母湯來完成辨認的過程。
文氏圖對於你解決廣泛領域內的問題當然是不夠的,但是它為你提供了一些展示類別包含和排斥關係的基本圖解方法。你可能會發現學習文氏圖的確有用。
命題邏輯
三段論只能應用於我們日常生活中遇到的很小一部分推理問題。更重要的方法是命題邏輯,它的應用範圍更廣泛。從公元前300年到公元1300年,哲學家和邏輯學家對於命題邏輯只是略有推進。自19世紀中期開始,邏輯學家開始在這一領域大放異彩,尤其是他們關注了諸如「且」與「或」這樣的邏輯用語。「且」的意思為聯結,例如,「A發生,且B發生,則A和B同時發生」。「或」的意思為非聯結,例如,「A發生,或B發生,則若A發生,B不發生」。在那個年代針對命題邏輯的工作成為後來計算機設計和編程的基礎。
在本章的開頭,我曾讓你來解決一個有關撲克牌的問題。你現在可以明白,那是一個需要使用條件邏輯來解決的問題。如果P發生,則Q發生。「如果一張牌的一面上有元音字母,那麼它的另一面上就是偶數。」在我們來仔細分析這個問題之前,我們先來看看下述問題。
你是一位警察局局長。你的工作之一是確保餐廳不向21歲以下的人出售酒。你的任務是挑出下列顧客中的一些人來檢查,看看他們是否遵守了規矩:「如果一位顧客喝酒了,則這個顧客至少為21歲。」你應當只檢查那些需要守這些規矩的顧客。
在第一張桌前,你看到了4位顧客。你看到:

你需要檢查:
a.顧客1
b.顧客1,2,3,4
c.顧客3和4
d.顧客1,3,4
e.顧客1和3
我敢肯定你會選擇c,檢查顧客3和4。現在讓我們回顧一下撲克牌的問題,我想很少有人在那個問題上選擇c,即牌3和4。我們能同意你的選擇嗎?其實這兩個問題的邏輯結構是相同的。請看下述我的邏輯。
撲克牌問題
保證遵守這個規則:元音?最好是個偶數在它的背面。
N—它的背面是否是偶數都無所謂。
4—它的背面是否是元音字母都無所謂。
A—它的背面最好是偶數。如果不是,規則就被破壞了。
3—它的背面最好不是元音字母。如果是偶數,規則就被破壞了。
餐廳問題
保證遵守這個規則:喝酒?最好是滿21歲了。
50多歲的顧客—無論是否喝酒都無所謂。
沒喝東西的顧客—是否滿21歲都無所謂。
喝了東西的顧客—最好是滿21歲了。如果沒有,那麼規則就被破壞了。
不到21歲的顧客—最好沒喝酒。如果喝了,規則就被破壞了。
如果沒有答對撲克牌問題,也不要灰心。只有不到20%的牛津大學學生解決了撲克牌問題的抽像版本。
為什麼撲克牌問題比餐廳問題困難這麼多呢?乍一看這有些奇怪,因為兩個問題都可以用條件邏輯來解決,事實上只要用最簡單的條件邏輯就行,即假言推理:
如果P發生,則Q發生。 如果顧客喝酒了,那麼他滿21歲了。
P事實上發生了。 顧客喝酒了。
因此,Q發生了。 因此,這位顧客滿21歲了。
假言推理引出了其否定式(如果Q沒有發生,則P沒有發生)。當Q(滿21歲)沒有發生但P(喝酒)發生了,就與條件規則產生了矛盾。
請注意,P(喝酒)對Q而言是一個充分條件,而非必要條件。即這是一種充分狀況,若要Q發生,則P發生。當然可能還有許多其他條件是充分的,要求這個人滿21歲才可以做,例如駕駛飛機或者賭博。
如果要滿足雙重條件,則若想讓Q發生,那麼P必須是充分且必要的條件。這樣就會出現(十分奇怪的)規則,如果你喝酒了,你就必須滿21歲,並且如果你滿21歲,你必須喝酒。
在對條件推理做了一些思考後,我們來看看為什麼喝酒問題很容易解決。
合理性、有效性和條件式的邏輯
正如我們所見,三段論式的論斷可以是有效的,即能夠正確表現出一種強有力的論斷形式,即便由此得出的結論是錯誤的。這種情況在命題邏輯中也會出現。
請判斷下述每個由兩個前提和一個結論組成的論斷是否是有效的。
論斷A
前提1:如果他死於癌症,那麼他患有惡性腫瘤。
前提2:他患有惡性腫瘤。
結論:因此,他死於癌症。
論斷B
前提1:如果他死於癌症,那麼他患有惡性腫瘤。
前提2:他沒有死於癌症。
結論:因此,他沒有患惡性腫瘤。
論斷C
前提1:如果他死於癌症,那麼他患有惡性腫瘤。
前提2:他死於癌症。
結論:因此,他患有惡性腫瘤。
只有論斷C是有效的。它符合假言推理:如果P(他死於癌症)發生,則Q(惡性腫瘤)發生。P(死於癌症)發生,因此Q(惡性腫瘤)發生。從論斷A和論斷B中得出的結論的合理性會讓我們有種感覺,即它們是有效的。然而,論斷A並不具有一種有效的論斷形式:如果P(死於癌症)發生,則Q(惡性腫瘤)發生。Q(惡性腫瘤)發生了,因此P(死於癌症)發生了。這裡出現了「相反的錯誤」,因為在推理過程中出現了倒置前提的情況,「如果P則Q」被換成了「如果Q則P」。(如果他患有惡性腫瘤,則他死於癌症。)如果有前提的話,我們的確能知道,因為Q發生了,P也發生了。然而,那並不是前提。
如果我們不能控制自己關注論斷的邏輯有效性的話,我們總會犯相反的錯誤。
相反錯誤1
如果車子不在我們的車庫裡,那麼簡進城了。
詹妮弗告訴我她在城裡看到簡了。
因此,車子不會在車庫裡。
然而,簡有可能利用了另外的交通工具進城去了,這樣的話,車子是有可能在車庫裡的。犯這樣的錯誤更有可能是因為一些特定的背景信息。如果簡很少在出門時不開車,那麼我們更有可能犯這種錯誤;如果她有時乘公共汽車,而有時由朋友開車載她出門,那麼我們犯錯誤的可能性降低。
相反錯誤2
如果我得了流感,那麼我會喉嚨痛。
我喉嚨痛。
因此,我得了流感。
然而,當然會有其他沒有得流感的可能性,比如普通感冒,或者鏈球菌性喉炎。如果人們迅速被流感擊倒,通常會有喉嚨痛的症狀,而沒有其他病痛發生,那麼我們更有可能犯這種推理的錯誤。如果流感、普通感冒和花粉過敏都在同一時刻發生,那麼我們可能不太會犯這種錯誤。
上述的論斷B是:如果死於癌症,那麼就患有惡性腫瘤;沒有死於癌症,因此就沒有患惡性腫瘤。這是一種反演錯誤。這種無效的論斷形式是,如果P則Q,P未發生,因此Q未發生。我們經常犯這類錯誤。
反演錯誤1
如果下雨了,那麼街道上一定是濕的。
現在沒有下雨。
因此,街道上一定不是濕的。
如果我們住在一個城市,這裡的街道清潔工人會頻繁地清潔(因此把街道弄濕),或者這是一個炎熱的夏天,因此消防栓有時是打開的,可供人們取水降溫,那麼我們犯錯誤的概率就比較低。如果我們住在亞利桑那州的鄉村,沒有街道清潔工,也沒有消防栓,那麼我們更有可能犯錯誤。
反演錯誤2
如果奧巴馬總統信仰伊斯蘭教,那麼他不可能是基督教徒。
奧巴馬總統不信仰伊斯蘭教。
因此,奧巴馬總統是基督教徒。
如果我們默認一個附加的前提,即人們只能信仰伊斯蘭教或者是基督教徒,則上述結論是有效的。當然,我們不這麼認為,但是我們可能會不由得相信這是奧巴馬僅有的兩個選擇,或者我們在討論時就覺得奧巴馬的宗教信仰選擇在這兩者之間。
關於相反和反演錯誤的一個有趣且重要的事實是,它們僅僅是演繹出的無效結論(即它們不是在邏輯上從前提條件推出的)。但它們可能是極好的歸納式結論(即如果前提是正確的,則結論更有可能是正確的)。「如果我喉嚨痛,則我得了流感」與「我喉嚨不痛,而我得了流感」相比,前者發生的可能性更大。如果沒有下雨,則街道是濕的可能性更小。在這些例子中,歸納式結論的合理性同樣也讓無效的演繹式結論的合理性提高了。
論斷形式和邏輯錯誤的例子不勝枚舉。然而,以上這些是其中我們最常犯也是最應當重視的錯誤。
實用推理模式
條件式推理的抽像形式——若P則Q——很難應用。我們經常以條件邏輯來推理,但是很少能完全利用它的抽像形式。相反,我們更可能會使用一種我稱為「實用推理模式」的方法,即一系列可用於日常生活場景的有用規則。本書中隨處可見這樣的規則。實際上,這也是本書的主要內容。有一些模式可以直接投射到條件邏輯上。這其中包括區分自變量和因變量的方法,以及相關性並不能證明因果關係這樣的原則。我們可以推演出沉沒成本原則和機會成本原則是有效的,而這是以一種有邏輯的方式從成本–收益分析中推出的。經濟學課程教授這些原則,然而它通常無法很好地向我們展示這些形式化的原則如何有效應用於日常生活中的推理。
一些實用推理模式可以投射到條件邏輯上去,卻無法有效推演出來,因為它們不能保證答案正確。實際上,它們一點兒也不關注命題的正確性或有效性,而只是評估一個人的行動是否恰當。這一邏輯分支被稱作道義邏輯(deontic),來源於希臘語詞根「deon」,意為義務。它解決的是一種包含了義務的情況,什麼會讓人獲得允許、什麼是可選擇的行為、什麼行為超出了道義的要求、什麼事應當做。契約模式是道義模式中的一種類型,它可用於解決大量與許可和義務有關的問題。
在分析喝酒年齡問題時採用的道義模式正是許可模式。你想喝酒(P)?那麼最好滿21歲(Q)。沒有滿21歲(非Q)?那麼最好別喝酒(非P)。
一種相似的模式是義務模式。如果你18歲了(P),你必須登記參與選舉(Q)。沒有登記參與選舉(非Q)?那麼你應該是沒到18歲,或者你沒有履行義務。
在法學院學習兩年會讓你的道義推理能力大有長進,而在哲學系、心理學系、化學系和醫學院,兩年的研究生學術訓練對此沒有任何幫助。
實用推理模式的第二種類型一點兒也不符合條件邏輯(或者說這種模式至少在貼合條件邏輯上十分不濟),然而這第二種類型可以廣泛應用於各種問題,並且能夠以純粹邏輯的形式被描述出來。應用這種模式需要邏輯思維,然而邏輯並不是讓它們變得強有力的東西,是這種模式本身的力量讓它在日常生活中閃閃發光。這其中包括了統計模式和具有科學步驟的模式,比如隨機控制設計。統計學和方法論的課程教授這些概念,但是並不能成功創造出這些實用模式,以幫助我們應對日常生活。社會科學和心理學專業的本科生和研究生課程的確推進了實用模式的應用,我們可以將統計學和方法論的模式在日常生活中使用,自然科學和人文專業就做不到這一點。其他應用性強的實用推理模式還包括奧卡姆剃刀原理、公地悲劇和應急概念,這些在第15章中將會討論。
最後,一些有力的實用推理模式並不具備抽像推理的潛質,而是僅僅具有實證原則,可以為日常生活中的大量問題提供正確的解決方案。這包括基本歸因謬誤,行動者和觀察者傾向於從不同角度解釋問題,損失厭惡,現狀偏見,從質量上來說一些選擇的結構優於其他的選擇,激勵並不必然是讓人們改變行為的最佳方式——比如換成本書中提到的其他行為方式。
抽像的實用模式是極其有用的,但是純粹的邏輯模式的效用十分有限。我相信情況的確如此,因為這個世界上有一種高度發展的文明,即中國的儒家傳統,這種思想傳統就沒有發展出單純的邏輯形式。有關這一文明的辯證傳統,及其現代新發展,將在下一章中展開描述。
小結
邏輯將有關現實世界推理的論斷抽像出來,這樣一個論斷的形式結構就能被單獨分析討論,而不受到先驗信仰的影響。形式邏輯,與這2600多年來的教育家的觀點相反,它並沒有關於日常生活想法的基礎。它主要是一種思維方式,能幫我們捕捉到一些推理過程中的錯誤。
一個結論的正確性和一個結論的有效性完全是兩碼事。一個論斷的結論有效,僅僅是因為它是按照一定邏輯從前提中推出的;而它是否正確,與「前提是否正確」或者「它是否是按照一定邏輯從前提推出」都無關。一個推定不一定非要從什麼前提中按照某種邏輯推斷出來,但是如果它是有邏輯的或是有實證支持的,那麼可信度會更高。
文氏圖體現了三段論推理,對於解決一些類別問題是有效,甚至是必要的。
在演繹推理中有時會出現錯誤,是因為它們對應的論斷形式被歸納起來是無效的。這是我們可能會犯推演錯誤的部分原因。
實用推理模式是推理的一些抽像規則,它是由許多思想綜合而來的。這包括了道義規則,如許可模式和義務模式。其中還包括了許多歸納模式,比如本書中討論過的統計規則,成本–收益分析,按照成熟的方法論步驟進行的推理。實用推理模式並不像邏輯規則那麼概念化,因為它只能應用於具體場景中,但是有些實用推理模式要依靠邏輯基礎。而像奧卡姆剃刀原理和應急概念,雖被廣泛應用卻與形式邏輯無關。當然,還有一些純粹是從大量實踐有效性中得到的實證歸納,例如基本歸因謬誤。