「湯姆森燈」〔得名於詹姆士·F·湯姆森(James F. Thomson)〕看起來與其他燈沒什麼兩樣,由一個按鈕開關控制。摁一下按鈕燈亮,再摁一下燈滅,再摁一下燈又亮。一個超自然的精靈喜歡這樣玩這盞燈:把燈點亮1/2分鐘,然後熄滅1/4分鐘,再點亮1/8分鐘,而後熄滅1/16分鐘,依此類推。「1/2+1/4+1/8+……」這個級數是我們熟悉的,它最終等於1。因此,到1分鐘的最後一瞬為止,這個精靈摁了無窮多次開關。在最後一瞬,燈是開著的,還是關著的?
每個人都知道,從物理的角度看這種燈顯然是不可能存在的。然而,我們的想像力並不受凡俗的物理學束縛,關於此燈的操作描述已經達到了最大可能的邏輯精確性。為了判定燈是開是滅,我們已經獲得了全部的必要信息——看來這是不可辯駁的。此外,燈要麼開要麼滅——看來這也是不可辯駁的。
然而,試圖解答湯姆森燈這個謎題是可笑的,因為這個問題等同於判定最大的整數是奇數還是偶數!
圓周率機
「圓周率機」更令我們不安。這是一種神奇的機器,其外觀像老式的收銀機。打開這台機器,它開始迅速地計算圓周率的各位數字(圓周率是直徑為1的圓的周長)。在古希臘、羅馬時代,人們就已經知道圓周率是一個無限小數:3.141 592 65……圓周率計算每一位數字所需的時間等於計算上一位數字的時間的一半,通過這種方法計算所需的時間得到壓縮。每當一位數字被確定,這個數字立刻會彈入機器頂端的一個窗口中。在任意一個時刻,只有剛剛得到的數字會出現在窗口中。
如果計算第一位數字需要30秒,那麼計算圓周率的所有數字所需的時間為1分鐘。[1]不僅如此,在1分鐘結束時,機器將如假包換地顯示出圓周率的最後一位數字!當然,這純粹是癡人說夢,因為圓周率的最後一位數字不存在。
第三台不可能的機器是皮亞諾機。這台機器像是一支自動伸縮笛,笛身上標有刻度,像尺子一樣。一端標有數字「0」,另一端標有數字「1」。一個游標從「1」端滑向「0」端,歷時1分鐘,勻速滑動。當游標經過的點的刻度為整數的倒數時,一隻機械嘴會讀出這個整數。隨著游標的滑動,聲調越來越高,同時,讀數字的速度越來越快。
例如,在這1分鐘剛開始時,游標位於刻度1,而1的倒數是1,機器用厚重的男中音朗讀「1」。30秒過後,游標位於刻度0.5處,0.5的倒數是2,機器朗讀「2」(聲音已經變成男高音)。又10秒過後,機器用女低音讀「3」。又5秒過後,是女高音的「4」。
在這1分鐘接近結束的時候,朗讀聲變得迅速而猛烈。聲調逐漸增高,尖銳到人耳聽不到的程度。有一陣子狗會發出嗚咽聲,狂躁地用爪子刨地……而後狗的耳朵也聽不見機器的朗讀聲了。在這1分鐘結束的時候,每個自然數都被這個機器朗讀出來了。
芝諾悖論
「無限」是一個用來表示這個巨大的、我們無法完全領會的世界的符號,它是悖論中極常見的主題。悖論中經常包含著無限對自鳴得意的日常世界的衝擊和威脅。
在最古老的關於無限的悖論中,有一些歸功於埃利亞的芝諾(生活於公元前5世紀)。芝諾在一本書中(大約寫於公元前460年左右)記錄了他的悖論,此書已失傳。芝諾好辯,樂於證明時間、運動以及其他我們習以為常的東西並不存在。他最著名的悖論是這樣的:善跑的阿基裡斯與烏龜賽跑。烏龜在阿基裡斯前面起跑,比方說,領先1米。為了追上烏龜,阿基裡斯必須先跑到烏龜的出發點。當他到達這個位置時,烏龜已經往前跑了一段較短的距離——10厘米。現在阿基裡斯必須再跑10厘米才能追上烏龜,但是與此同時,烏龜又往前跑了1厘米。以上分析過程可以無窮延續,烏龜領先阿基裡斯的距離會越來越短,但是阿基裡斯永遠也追不上烏龜。
芝諾否認無窮數列和無窮量的真實性。他認為,如果你可以表明某個東西涉及無窮,你就可以證明這個東西是不存在的。在現代人看來,芝諾的某些論證缺乏說服力。芝諾的表現就像是一個永遠拒絕無窮級數的頑固、古怪的數學家。阿基裡斯必須跑的距離構成了一個無窮級數,加起來等於111.111……厘米(即111又1/9厘米)[2],這是一個有限數。所謂的「無限」只是芝諾分析的結果,並非物理意義上的無限。
在芝諾發明的悖論中,「飛矢不動」悖論更令人困惑。一支箭在空中飛過。在時間歷程中的任意一個瞬間,這支箭是靜止的。在這個瞬間,箭就像處於一張靜止的照片中,或者說,就像是從拍攝飛箭的電影中截出的一個孤立的畫面。時間是由無窮多個這樣的瞬間構成的,既然在每個瞬間箭都是紋絲不動的,箭的運動又何在?
飛矢不動悖論值得深入思考。我們把這個問題移植到現代語境中。假設有一支箭,它是由原子構成的。它在相對論情境下的時空中運動,我們在一個慣性參照系中對它進行測量。在這種表述中,我們以日常含義使用「時間中的一個瞬間」這個詞組,和芝諾一樣。我們依然接受因果關係:將來是由現在決定的,而現在是由過去決定的。(除了在量子層次上——我們可以暫且忽略這種考慮吧?)在完全靜止的一個瞬間,一支飛行的箭與一支靜止的箭有何不同?看來這支運動的箭上一定附著了一些信息以區別於靜止的箭。否則,它怎麼「知道」在下一個瞬間會疾射向前?
就本書的討論範圍而言,我們更關注當代人的「無限機器」悖論。這些悖論是在芝諾的啟發下誕生的。他們質疑的是知識,而非運動學。關於無窮級數的現代理論無助於解答這些問題。每台機器的操作都屬於超級任務,其動作涉及無限。然而,這些動作可以被清晰地描述——儘管完成動作本身也許是不可能的。在每個例子中,超級任務允諾我們瞥一眼不可知的事物——例如希臘神話中的美杜莎。[3]
注重實際的人也許會對無窮機器的想法表示質疑。關於超級任務的哲學討論就好比醫生為一種並不存在的疾病尋找療法。然而,超級任務可以和真實世界中的某些過程類比。這些問題表現出來的奇特狀態只有通過由一系列離散的動作組成的無窮(或接近無窮)的序列才能得到解答,這是值得研究的。
造一盞湯姆森燈
關於無窮機器的某些討論關注操作細節。雖然機器的實用性似乎與討論無關,但是略微分析一下細節也許有助於發現其中的邏輯困難。阿道夫·格林鮑姆(Adolf Grunbaum)分析了這三台機器。
針對湯姆森燈的一種反對觀點是,電燈泡不可能無限且迅速地被打開、熄滅。在操作過程中的一個過去的確定時刻,當電流接通時燈絲沒有足夠的時間完全被加熱,而當電流斷開時燈絲沒有足夠的時間冷卻。在最後階段,燈絲可能始終處於半明半暗的狀態。
此外,每個人都知道,連續開關電燈泡很容易把燈泡燒壞。湯姆森燈的燈泡一定會燒壞。
阿道夫·格林鮑姆認為,這些討論都沒說到點子上。問題的關鍵是,在這1分鐘結束時,燈泡是亮的還是滅的?即使燈泡燒壞了也不要緊,在這1分鐘過後,我們總可以卸下壞燈泡,擰上一個新的,看看它亮不亮。
真正的問題在於開關。湯姆森燈的開關按鈕在每一次打開或關閉時,顯然要經過一段距離。因此,按鈕必須在有限的時間內經過無限的距離。一個物理上的限制足以提出反駁:在這1分鐘接近結束時,按鈕的運動速度一定會超過光速,而這是不可能的。
按鈕將往復運動無限距離的這個問題並不重要——實際上,按鈕不需要走這麼遠。格林鮑姆和艾倫·賈尼斯(Allen Janis)做了一點改進,得到了升級版的湯姆森燈。改進之後的情況更有道理。
把按鈕畫成一個垂直的圓柱,其底部是導電的。當按鈕被完全摁下時,圓柱的底部接觸電路的兩個裸露電極,電流流過圓柱底部,點亮燈泡。
每當燈應當點亮時,按鈕接在連通的電路上;每當燈應當熄滅時,按鈕以恆定的速度沿上下方向做一個短程運動。每一次按鈕彈起的距離僅限於時間允許的範圍內,而運動速度是固定的。
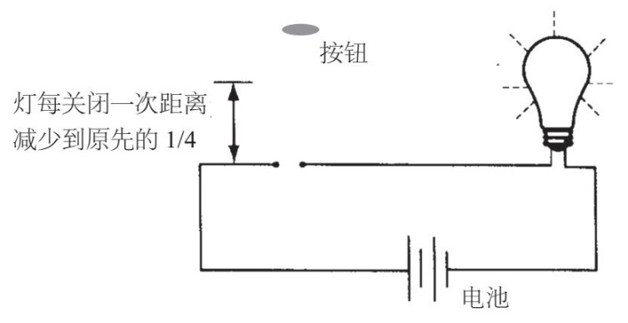
在最初的30秒中,按鈕壓在電極上,燈泡是亮的。再過15秒,燈泡關閉。按鈕先用7.5秒向上彈起,又用7.5秒回落。然後,按鈕在電路上停留7.5秒,這段時間電路接通,燈泡又亮了。再往後,按鈕用1.875秒向上彈起,用1.875秒回落,燈泡保持熄滅3.75秒。
按鈕起落無窮多次,但是每一次移動的距離都是上一次的1/4,就像是一隻彈性不大好的球。在整個操作中,按鈕移動的總距離同總時間一樣,是個有限數。移動速度是常數,比光速小得多。
遺憾的是,格林鮑姆和賈尼斯的改進還是不能徹底挽救湯姆森燈。按鈕在往復運動的過程中需要加速和減速,而加速度會超過任意的固定值。看起來,無限大的加速度畢竟比無限大的速度容易接受,但是……任何物理對象都只能承受一定限度內的加速度。在某一時刻,加速度肯定會摧毀按鈕,其效果就和用錘子砸碎的效果一樣。
改進版的湯姆森燈有一個更嚴重的問題:在1分鐘之後燈是開是滅已經不是問題。在操作過程中,按鈕的底部與電路之間的距離越來越小,最終恰好停在電路項上。(就好像一隻球在地板上蹦,最終落在地板上。)改進版的湯姆森燈在操作結束時一定是亮的。修改開關的結構就會導致這種令人不滿的結果。這個改進版的湯姆森燈與原來的湯姆森燈有關係嗎?——確實成問題。
在設計圓周率機和皮亞諾機時也會遇到一些問題,有的與上面的問題類似,有的則不是。〔順便說一句,皮亞諾機的名字是格林鮑姆起的,是為了紀念意大利數論家朱塞佩·皮亞諾(Giuseppe Peano)。〕圓周率機的問題是,計算圓周率的數字的過程怎麼可能這麼快。下文將提到,計算速度如同運動速度一樣,是有上限的。在數字向窗口中彈出的過程中,為了避免運動速度達到無限,運動的距離必須遞減。最終,我們將無法判斷正在顯示的是哪個數字。圓周率機可以換一種顯示模式,每個數字被打印出來,數字的字體表現為超現實主義風格:每個數字的高度是上一個數字的一半。全部計算結果可為一張索引卡片所容納。但是有一個問題:即使用最強大的電子顯微鏡也看不出最後一位數字是幾。
皮亞諾機有一個獨特的問題:數字的讀法越來越複雜。乾淨利落地讀出一個100位的數也要花很長時間。賈尼斯建議不採用日常語言的讀法。他的方案是,設計一個編碼方法,讓每一個數對應一個頻率確定的音調,然後用哨音把數字「吹」出來。
發出一個聲音需要消耗多少能量取決於頻率(音調)和振幅(音量)。為了避免能量需求達到無窮大,隨著頻率的增加,振幅必須減小。在這1分鐘的最後一瞬,機械嘴的音量將下降到0。你無法聽到最後的哨音——即使你的耳朵有能力捕捉音調無限高的聲音。
請注意:如果試圖以更具物理上的可實現性的方式設計三種無限機器中的任何一種,都會導致一個結論——最後的結果是不可見的(或不可聞的)。許多哲學家認為,在涉及無限機器、超級任務以及只有通過超級任務才能瞭解的事實時,總是有些可疑的東西。
幾何級數
無限——完全就其本意來說是不可理解的,但是趨近於無限的情況隨處可見。有一個印度傳說,什裡姆國王(King Shirim)曾經落入西薩·本·達希爾(Sissa Ben Dahir)的圈套。達希爾是國王的大臣,發明了國際象棋。國王鍾愛這一遊戲,決定重賞發明者。因為國際象棋棋盤有64個格子,國王決定為每個格子賞賜達希爾一塊金子。達希爾禮貌地謝絕了這份賞賜,懇請國王以另一種方式獎勵他。他請求國王在棋盤的第一個方格上放一粒麥子,在第二個方格上放兩粒麥子,在第三個方格上放四粒麥子,依此類推,每個方格上的麥粒數是上一個方格的2倍,直到棋盤的每一個方格上都分配了麥粒。
因感動於達希爾的謙虛,國王收回成命,轉而下令拿來一袋麥子,按照達希爾的要求仔細地數出麥粒來。當國王的僕人們對付第12個方格時,他們就已經無法把所有的麥粒放進方格裡了,只好把大臣應得的麥子在棋盤旁堆成一堆。國王吃驚地發現,第20個方格還沒被滿足,一袋麥子就耗盡了。他下令取來更多的麥子……最後所有的麥子都用完了。他的王國的所有麥子加在一起也無法滿足達希爾的要求,不僅如此,全印度乃至全世界的麥子加在一起也不夠用。
這個故事的寓意在於,永遠不要低估幾何級數。當然,從民間故事裡挖掘出數學含義有點奇怪。根據國王最初的想法,賞給達希爾的金子直接和棋盤包含的方格數成正比。如果達希爾設計的棋盤不是64個方格,而是81個、49個或者其他數字,從國王的角度說都沒有太大的差別。區區幾塊金子與國王的財富相比,算得了什麼呢?
然而,幾何級數的增長超出世間的任何限制——對於財富或任何其他東西都是如此。達希爾要求以麥粒為單位來賞賜,麥粒的價值與金塊相比微不足道,但是這個事實對最終結果幾乎沒有影響。
我們看一下,多少粒麥子才能滿足達希爾的要求。這個總數是1+2+4+8+…,換一種寫法,即20+21+22+23+…262+263。(這個級數的最後一位是263,不是264,因為第一個方格中的麥粒數是20,即1。)
以2為公比的幾何級數的和總是等於最後一項的2倍減1,再用這個差乘以數列的第一項。例如,20+21+22(=1+2+4)等於23減1(即8減1)。所需的麥粒的總數是264–1,等於18 446 744 073 709 551 615。
1噸麥子大約包含1億粒麥粒,因此,所需的麥粒總量大約為2 000億噸。現在(指本書成書時的1987年)全世界小麥年產量僅有4.6億噸。國王欠下達希爾相當於4個世紀的小麥產量的債務(以現在的年產量計)。顯然,當時的小麥產量還比現在低得多。(我們不知道這個故事發生在多久以前,因為國際象棋的發明時間不能確定。和籃球一樣,國際象棋發生過幾次變革,此外,我們不知道歷史上是否確有達希爾其人。)
馬爾薩斯災難
托馬斯·馬爾薩斯(Thomas Malthus)認識到,世界人口以幾何級數增長,而糧食產量僅以算術級數增長,在此基礎上形成了他的著名理論。馬爾薩斯有理由相信,每年新開墾的農田面積是固定的。因而,糧食供給的增長大致是這樣的:100,102,104,106……另一方面,人口的增長率(主要取決於每年的新生嬰兒數)隨人口規模本身而增長。世界人口趨向於每隔若干年增加一倍,增長情況大致是:1,2,4,8,16,32……和達希爾的獎賞一樣,這是一個幾何級數。馬爾薩斯警告說,人口增長必定超過食物供給,導致全球性的饑荒。
用「幾何級數」這個術語來稱呼這種級數並不恰當,把這種級數以幾何指稱既不形象又容易引起混淆。一個更恰當的術語是「指數級數」,這個名稱源自「指數」這個術語。生長的有機體一般以指數增長為特徵。無論是細菌的繁殖還是人類的繁衍,其共同特徵是,新增個體數與總數成正比。復利存款也呈指數增長——這顯然與這一事實有關:借方和貸方都是不斷生長的有機體,他們創造了以指數狀態增長的經濟,而且,他們進行交易時依據的貨幣處於呈指數增長的通貨膨脹中。
指數增長可以用簡單的數學函數描述。所謂函數是從一個數轉換為另一個數的過程。你可以把函數理解為袖珍計算器上的一個特定的鍵。你先在計算器上輸入一個數,然後摁這個鍵,得到一個新的數。例如,開平方函數(許多計算器上都有開平方鍵)會產生一個數,此數乘以自身後得到最初輸入的那個數。如果先輸入36,再摁開平方鍵,得到6。
函數不僅限於可以在計算器上算出。任何一個從某個數產生新數的清楚而確定的過程都是「函數」。我們可以定義一個函數:67乘以n的積加上381(對於任意數,n),這就是一個有意義的函數。函數通常用方程的形式表示,例如:
f(n)=67n+381
「f(n)」讀作「n的函數」。
我們很自然地想知道,哪種動物最大、什麼動物的運動速度最快。同樣,數學家也想知道,哪一種函數最大,或者增長得最迅速。有些函數勝過其他函數。如果在n足夠大時,一個函數的值總是大於另一個函數,那麼我們說前者比後者大(或者說增長更快)。例如,函數A是A(n)=1 000 000 000 000 000,而函數B是B(n)=n,則在很大一段區間裡b較小。但是當n取大於1 000 000 000 000 000的任意數時,B(n)都大於A(n)。因此,B(n)的增長比A(n)快。
以上這些函數都不算大。任何一個常函數,即f(n)等於一個固定值的情況,最終一定會被一個與n成正比的函數超過。同樣明顯的是,這兩種函數都會被與n2成正比的函數超過。與n3成正比的函數最終會增長得更快。類似地,對於與n4、n5、n6等成正比的函數,也是如此。
多項式是一個表達式,由一個變量的各次冪組成,例如n3+8n2–17n+3。一個多項式表示了一個函數。粗略地說,一個多項式函數的相對增長速度取決於它的最高次冪。函數n3+8n2–17n+3的增長速度遠遠超過任何最高次冪為2的函數。同理,它將被一個最高次冪為4(或更高)的函數超過。
許多函數的增長還要更快。馬爾薩斯的悲觀論點立足於一個事實:指數函數的增長超過任何多項式函數的增長。在一個指數函數中,某一個特定的常數以n為指數(而非n以某個常數為指數)。f(n)=3n是一個指數函數,它表示3自乘n次。當n為2時,3n即32,等於9。當n為1時,結果即等於底數(這個例子中是3);當n為0時,無論底數是多少,結果都定義為1。於是,對應0,1,2,3,4……的函數值分別為1,3,9,27,81……每一項的值等於前一項的3倍。底數越大,函數值的增長越快。對於10n,每一項是前一項的10倍;而對於1 000n,每一項是前一項的1 000倍。
在複雜性理論中,表示一個問題的困難程度的最常用的標準是解決此問題所需的時間。不用說,每個人的工作效率是不一樣的,計算機也各不相同。同樣重要的是,針對同一個問題,算法可能不止一種,而某些算法比其他的更快。解決各種類型的問題所需的時間差異如此之大,這使得計算機與計算機之間(以及人與人之間)的計算速度的差別已經不重要了。
需要強調的是,某些問題可以用「多項式時間」解決,而另一些問題需要「指數時間」。這意味著,解決一個問題所需的時間可以表達為關於問題的規模(或複雜度)的一個多項式函數(或指數函數)。如果一個問題需要指數時間,則通常會令人絕望。無限機器也許只是胡思亂想,但是指數時間問題卻是真實而普遍存在的。解決這類問題需要數量接近於無窮多的步驟——即使問題出現在有限的宇宙中。
下一章將討論多項式時間問題與指數時間問題的差別以及這個問題與悖論的關係。現在,我們來研究兩個質疑時空無限性的悖論。
奧爾貝斯悖論
1826年,德國天文學家海因裡希·威廉·奧爾貝斯(Heinrich Wilhelm Olbers)意識到宇宙中有些東西似乎不對勁。天文學作為科學的一個分支,不能迴避無限的問題。物理宇宙要麼是無限的,要麼是有限的。但是對於大多數人來說,這兩種可能性都不容易被接受。
布萊士·帕斯卡(Biaise Pascal)寫道:「每當設想我的生命被封閉在永恆的時間中的一個狹小的範圍內,我能看到且感知的一小部分空間淹沒於一個無限廣袤的空間中,我對這個無限的空間一無所知,這個無限空間也不能瞭解我。一想到這些,我就對自己身處於此地而非別處感到恐懼和震驚。」另一方面,一個有限的宇宙也許令人更加難以接受。人類難以設想空間怎麼會有盡頭。
這種不安並非新問題。希臘哲學家盧克萊修(Lucretius)認為,他的論證足以證明空間是無限的:假定空間是有限的,那麼空間則有一個邊界。如果讓某個人達到這個終極的邊界,把一支標槍擲過邊界,那麼這支標槍要麼穿過邊界,要麼被什麼東西擋住——某個本身必定在邊界外的東西擋住了它。無論是哪一種情況,都說明在邊界外存在某種東西。以上操作可以不斷重複,推動這個所謂的邊界無限倒退。
在奧爾貝斯的時代,大多數天文學家認為空間的無限性是理所當然的。奧爾貝斯對無限時空的反對被當作癡人說夢,他也因此而聞名。假定宇宙是無限的,而星體(還有星系,雖然奧爾貝斯那個時代的人還不知道星系)在各個方向上從中心向外無限延伸出去。在這種情況下,從地球發出的一條直線(無論其方向如何)必將與一顆星體相遇。
當然,這條直線也許在延伸數十億光年之後才與某星體相遇。關鍵在於,在一個散佈著星體的宇宙中,這條直線最終必定遇到一個星體。這就好比,如果我們在輪盤賭上玩足夠長的時間,那麼所有號碼最終肯定都會出現,不會有例外。
太陽是一顆恆星,在天空中,看起來有寬度的恆星僅此一顆。如果太陽與我們的距離增加到現在的10倍,那麼它的外觀表面積將只有現在的百分之一,亮度同樣下降到之前的百分之一(根據很久以前就已確立的亮度遞減公式)。如果太陽距離我們比現在遠100萬倍,它將變暗1萬億倍,它在天空中的大小將是現在的一萬億分之一。需要注意的是,在天空中,單位面積上的亮度保持不變,與距離無關。無論太陽距離地球多遠,其單位表面積上的亮度都是固定的。奧爾貝斯意識到,這個簡單的事實蘊含著一個悖論。
在夜空中,其他星體只呈現為針孔大小,但是這些針孔(平均而言)與太陽表面一樣亮。光沿著直線傳播,如果從地球出發的一條直線與某顆星體相遇,我們可以見到這顆星體發出的光。如果從地球出發的每一條直線都與某顆星體相遇,那麼整個天空應當充滿相互交疊的星體光盤,每個光盤都與太陽的光盤一樣明亮,所有光盤交疊在一起,遍佈整個蒼穹。這幅圖景就好像太陽是一個空心的球體,而我們位於球體的中心。陰影之類的東西不會出現,也不會有所謂的夜晚——夜晚其實就是陰影。
太陽無處不在,陽光永恆地照耀。也許你會認為,某些黑暗的對象會擋住星光,讓我們無法看見。但是在這種環境下,不可能有任何黑暗的東西,所有東西都會吸收、傳播或反射光(通常三種情況都有),任何吸收光線的東西(如月球、星塵、這本書、你的眼瞼)都會吸收熱量,直到其溫度達到星體本身的平均溫度,而後他們將發出同樣強度的光。任何完美地傳播光線的東西(一塊理想狀態下的玻璃)都是完全透明的,不會產生任何陰影。那些反射光線的東西(比如鏡子)應當反射出與背景同樣耀眼的光,讓我們分辨不出來。
這就是奧爾貝斯悖論。當然,整個論證顯然是錯誤的。這個悖論令奧爾貝斯聞名,但他並不是最早沿著這個思路設想的人。托馬斯·迪格斯(Thomas Digges)、埃德蒙·哈雷(Edmund Halley)、埃德加·愛倫·坡(Edgar Allan Poe)以及其他人也曾關注過這種觀點,但是它在幾個世紀的時間裡一直沒有受到重視。顯然,和前文討論的無限機器一樣,這個悖論針對一個無限性的問題(宇宙是否無限)提供了一個短平快而輕佻的答案。
反對「多」
把望遠鏡倒過來看,你會見到有趣的圖景。類似的想法可以導致一個悖論,這個悖論可視為芝諾「反對『多』的悖論」的升級版。我們知道,即使最短的線段也包含著無窮多個點。這麼說,一個核桃殼內部也存在著無限的空間,如同遼闊的星際一樣不可測量。
「堅固」的物質是由原子構成的,而原子內部大部分是未被填充的空間。非空的部分是質子、中子和電子,而這些粒子內部大部分也是未被填充的。如果空間是無限可分的,就會有一個無窮的序列:粒子、亞粒子、亞亞粒子,而它們內部大部分是空的。也就是說,任何東西內部的99.999 999%以上的空間都是虛空。果真如此,我們就應當無法看見任何東西,如同格特魯德·斯坦(Gertrude Stein)提到「奧克蘭」一樣——那兒什麼也沒有。
利用物理學可以簡單地解決這個悖論。一方面,原子中的電子會散射可見光。電子可以像波一樣在空間中展開,實際上,整個原子被電子「籠罩」和「覆蓋」著。另一方面,電子可以被當作一個無限小的粒子,永遠無法進入其內部。原子核中的質子和中子不散射普通光。[4]
為了使這個悖論成立,我們必須假定自己有一種超級視力:當且僅當從你的眼睛出發的一條絕對直的幾何直線遇到一個被物質佔據的點時,你就會看到東西。這樣,當你看一個核桃殼時,你看到的不是核桃殼,而是成千上萬的由電子和組成電子的夸克(或者組成電子和夸克的終極的亞粒子)構成的點。每個東西看起來都像是不規則的塵埃碎片。由於我們看不到單獨的、無限小的點,所以每個東西都應當是不可見的。
奧爾貝斯悖論的解決
現在回到奧爾貝斯的宏觀悖論。關於這個悖論的任何解決方案都必須立足於三個前提:宇宙是無限的;星體隨機分佈;沒有任何東西能夠阻止遠方的星體發出的光被我們看到。這三個前提是預設的。
一種解決方案是,假定星體的分佈類似於上一節討論的亞原子物質的分佈。這兩個悖論交相輝映,合在一起考慮則兩個問題都可解決。為了解決奧爾貝斯悖論,瑞典數學家沙利耶(C. V. L. Charlier)提出,星體不是任意地散佈在各處,而是聚集在層次分明的體系裡。現在我們知道,我們附近的星體都屬於一個星系——銀河系,而銀河系本身是一個星系群(本星系群)的一部分。本星系群是一個更大的結構體的一部分,這個結構被稱為本超星系團。這個本超星系團又是雙魚座—鯨魚座超集結綜合體的一部分……如果有一天有人宣佈雙魚座—鯨魚座超集結綜合體是一個更大的物體的一部分,我們也不會太吃驚。
沙利耶表明,在這個無窮無盡的層級結構中,即使星體的數量是無限的,悖論也可以避免。例如,也許某個由星系構成的超超超星系團離我們過於遙遠,以至於在我們的天空中,它的圖像恰好被隱藏在大角星或參宿四之類的微小天體後面。應當有一些超超超星系團和超超超超星系團距離我們極其遙遠,這使得它們看起來甚至更小。根據沙利耶的設計,在大多數方向上,我們的視線無限延伸以後也碰不到一顆星體,因此,夜空是黑暗的。
從幾何的角度看,沙利耶的解釋是可以成立的。唯有一個原因使這個理論失敗:它似乎無法解釋已經觀測到的天體層級結構的相對距離和大小。附近的星系雖然朦朧模糊,但是比附近的恆星大得多。仙女座星系非常昏暗,但是視直徑是太陽或滿月的數倍。南方天空的麥哲倫星雲(距我們的星系最近的兩個星系)的大小相當於一顆距我們一臂長的檸檬的大小。附近的星系團甚至更大。例如,肉眼不可見的室女座星系團佔滿了整整一個星座區域。
現代人對奧爾貝斯悖論的解決訴諸一個20世紀以前還不為人知的事實:宇宙處於膨脹中。所有我們可見的星系都在以巨大的速度遠離我們的星系。我們無法直接測量這種運動,但是它造成了從這些星系發出的光的改變,我們接收到的光透露了關於運動的信息。如果不假設這種運動,這種光的變化是無法解釋的。位於天空中每一個確定區域的星系都在離我們遠去;在地球另一面的天空中,星系也在離我們遠去,只不過方向相反。
對這一現象的一種解釋是,我們的星系是「特殊的」,它處於宇宙的中心。另一種解釋同樣可以很好地解釋這個現象:整個宇宙都在膨脹。這種說法很方便,但是有點兒容易引起誤解。這種膨脹不是龐加萊所說的那種完全均勻的膨脹,而是以長度標準不變為基礎的膨脹。地球和銀河都沒有變大,也許甚至本星系群也沒有變大。但是星系團之間的距離卻越來越大。從理論上說,我們可以用尺子測量星系間的距離膨脹值,因為尺子並沒有膨脹。
根據宇宙膨脹假說,不需要假定我們的星系或它在宇宙中所處的位置有何獨特之處。那些在遙遠的星系中的居民也會發現,自己處於膨脹「中心」。這個假說不需要假定我們的星系是特殊的,由於少了這個無關要求,所以這個假說更好。
我們所知的、距我們最遠的星系在以接近光速的速度遠離地球。一個高速遠離的物體發出的光會產生「紅移」:光的波長增大而能量減小。能量較高的可見光在紅移以後變成能量較低的微波。當一個發光體以接近光速的速度遠離時,它發出的光能量將下降到幾乎完全消失的程度。因此,我們接收到的非常遙遠的星系的光能量非常微弱,以至於不可見。
我們來看一下以上知識對奧爾貝斯悖論的論證有何影響。設想我們把整個宇宙空間劃分為以地球為中心的一系列同心球殼層。由於光的強度與距離的平方成反比,我們從各個殼層接收到的光(平均而言)強度相同。所有距太陽系10光年以內的星體發出的光應當與距離在10光年至20光年之間的星體發出的光強度相同。距離在30光年至40光年之間的星體,乃至於距離在1 000 000光年至1 000 010光年之間的星體也是如此。
如果宇宙是無限的,所有這些光的總量是一個無窮級數的和,大致為x+x+x+x+x+…,其中x表示從每個殼層發出的光。這種類型的無窮級數不收斂,求和時便會推出無限。
但是,由於來自更遠的殼層的光受到紅移效應的削弱,以上圖景全變了。星系距我們越遙遠,它遠離的速度越大,光的能量越小。因此,這個無窮級數會更像這樣:x+0.9x+0.81x+0.729x+0.6561x+…,其中每一項按固定的比例遞減。這樣的無窮級數是收斂的。有無窮多的星體照耀地球的天空,而光的總量可以依然是有限值。
很少有宇宙學家懷疑這個悖論可以用宇宙膨脹合理地解釋,但是還存在一個更簡單的解釋。1720年,埃德蒙·哈雷(Edmund Halley)寫道,天空的黑暗反駁了星體有無限多的觀點。今天,許多宇宙學家相信宇宙確實是有限的(雖然他們的出發點不同於奧爾貝斯悖論)。廣義相對論提供了一種解釋,使得有限的宇宙不必有一個令人難以接受的「邊界」。空間自身是可以彎曲的,這個三維結構可以類比成一個球的表面。在地球上,如果你走得足夠遠,無論朝哪個方向,你都會回到出發點。空間本身也許同樣如此:一艘火箭如果沿一條直線飛行得足夠遠,它將回到發射點。
根據大多數當代宇宙模型的預言,如果宇宙中的物質密度達到或超過一個確定的限度,那麼宇宙就是這樣一個有限的宇宙。已觀察到的可見物質(星體)的密度低於這個限度,但是據推測,存在著足夠多的不可見物質(星際間的氫、黑洞、中微子?)以建立一個有限的宇宙。關於遙遠的星系和類星體的「引力透鏡」效應的研究支持了有大量不可見物質存在的想法。
特裡斯特拉姆·香迪悖論
人們對待時間和空間時,會在潛意識裡使用雙重標準。時間的無限性似乎與空間的無限性略有不同。我們很自然地認為,空間向各個方向無限延展(或許這是文化傳承的結果?),而時間則被認為僅在未來的方向上是無限的。我們追問時間的起點,但是很少追問空間的起點。
「時間在過去的方向上是無限的」並不是一種廣為接受的觀點。不過,這個觀點可以「回答」「世界是何時以及如何被創造的」之類的問題,因為如果時間在過去的方向上是無限的,那麼這類問題就是無意義的。相反,「時間在未來的方向上是無限的」這個觀點則得到了普遍接受,甚至那些以先知預言為基礎的宗教都願意接受這個想法。千年盛世到來後,善者永生,或者在一個新的世界中輪迴。即使某些極端虛無主義的教派相信,時間有一個真實的終點,在終點處萬物歸復於虛無,與時間的起點之前完全相同,只有時間本身是善的——即使這種信仰存在,也是非常罕見的。
羅素的特裡斯特拉姆·香迪悖論(Paradox of Tristram Shandy)巧妙地利用了「無限未來」這個概念。特裡斯特拉姆·香迪是勞倫斯·斯特恩(Laurence Sterne)18世紀60年代的漫遊小說《香迪傳》中的健談的故事講述者。羅素寫道:「如我們所知,特裡斯特拉姆·香迪用了兩年時間來記錄他的生活中的頭兩天的歷史,然後他抱怨道,按照這種速度他永遠也寫不完。但是我認為,如果他可以永遠活下去,而且堅持不懈地寫下去,那麼,即使他的一生始終像文章開端那樣充滿需要記錄的內容,他的傳記也不會遺漏任何部分。」
羅素的論證大致是這樣的:假定香迪生於1700年1月1日,而寫作開始於1720年1月1日。在第一年(1720)寫第一天(1700年1月1日)的事,寫作進程如下:

每一天對應一年,每一年對應一天。如果香迪的寫作工作持續至今,到1988年,他將進展到1700年9月的事件。按部就班且不死的香迪將在大約106 840年時記錄下今天(即本書作者寫下本段的日子)的事件。對於任何一天,香迪在未來都有指定的一年去記錄它,絕無例外,因此,羅素說:「他的傳記不會遺漏任何部分。」即便如此,香迪的寫作工作將越來越滯後。他每寫一年,距離最後竣工就遠了364年!
羅素的論證以喬治·康托爾(George Cantor)的無窮數理論為基礎。如果在兩個無窮量之間可以建立起一一對應關係,則這兩個量相等。例如,數學家認為,所有正整數[5](0,1,2,3,4,5…)的個數與所有偶數(0,2,4,6,8,10 …)的個數相等,雖然有些人可能認為,前者是後者的2倍。二者相等,因為任何一個正整數n可以與一個偶數2n配對,而如此配對不會遺漏任何偶數。
更令人費腦筋的是克雷格(W. L. Craig)提出的一個悖論,這個悖論是特裡斯特拉姆·香迪悖論的顛倒版。假定時間在過去的方向上是無窮的,而香迪已經寫了無窮長的時間。克雷格指出,在這種情況下,在年與日之間仍然存在康托爾式的一一對應。香迪應當剛剛完成他的傳記的最後一頁。但這是荒唐的。既然他要花費一整年的時間記錄昨天的事件,他怎麼可能已經把昨天的事件記錄完了呢?
克雷格以及其他人用這個顛倒版的悖論證明,無限的過去是不可能的,雖然這個證明不那麼令人信服。羅賓·斯莫爾(Robin Small)針對顛倒版的香迪悖論提出了一個合理的答案。答案是:實際上在特定日和特定年之間不可能建立一一對應。
假定現在是1988年12月31日午夜,香迪剛剛完成他的手稿的最後一頁。在過去的一年裡,香迪記錄的是哪一天的事?不可能是這一年中的某一天。(否則就意味著,在這一年中這一天以前的時間裡,香迪已經開始記錄尚未到來的一天。)在1988年,他可以記錄的最鄰近的一天是1987年12月31日。
如果香迪用1988年記錄1987年12月31日,那麼他必須用1987年記錄1987年12月30目,這又是不可能的。實際上,在1987年他不能記錄1986年12月31日以後的任何一天。
但是,如果他在1987年記錄1986年12月31日,那麼他不得不在1986年記錄1986年12月30日……我們可以設想的任何一種對應方式都會遭到反駁。所謂的香迪一直在寫的那一天將向過去無窮倒退。它不可能是任何一天。
結論:如果過去的時間是無限的,而香迪始終在寫,那麼他將留下無窮多的未完成的寫作任務。他最近完成的部分記錄的是無窮遠的過去的事件。
實際上,羅素版的悖論和克雷格版的悖論都不難解決。羅素從來沒說香迪終將完成他的手稿。羅素的意思是,我們無法找到香迪不能記錄的一天。香迪的「最後」一頁始終是一個遙不可及的海市蜃樓。
[1] 在一間屋子裡同步運行圓周率機和湯姆森燈,屋子裡沒有其他光源,在閃爍的燈光的照明下可以見到圓周率的所有奇數位數字。
[2] 這是一個等比數列,首項為100,公比為1/10,因此前n項之和為100(1–1/10n)/(1–1/10),當n趨於無窮時,結果即為111又1/9。——譯者注
[3] 美杜莎為希臘神話中的女妖,任何人看她一眼都會變成石頭。美杜莎是不能看的,所以「弊一眼」美杜莎是不可能的,作者以此類比「超級任務」,說明超級任務是不可能完成的。——譯者注
[4] 原著此處有筆誤,譯文已更正。——譯者注
[5] 原文為「整數」,應為筆誤。——譯者注
