復合命題的真值可以通過真值表確定。為了構造一個復合命題的真值表,首先要找出相應公式中的簡單命題。然後,按照這些簡單命題在公式中出現的順序,把它們寫在真值表的左上方。接著,以與上述相同的方式給每個簡單命題指派真假值。最後,使用2n來計算行的總數。例如,F ·~C的真值表是:
例11-62
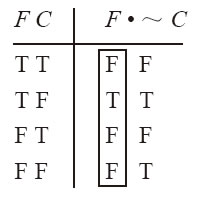
位於這個真值表右側的公式是F和~C的合取,前者的值在左側第一欄,後者的值是需要首先確定的。我們通過把否定式的真值規則應用於左側第二列的每一行而得到~C的值。一旦確定了~C的真值,我們就把它們填入右側的波浪符下方。然後,把合取式的真值規則應用於F的值(位於真值表的左側)和~C的值(位於波浪符下方),而得到該合取式的真值。我們把所得到的值寫在合取符號(點)的下方,並用一個方框加以標記。在主聯結詞下方的這一列是最重要的,因為它提供了關於F·~C這一復合命題的真值的信息。它告訴我們這個復合命題為真,僅當「F」和「~C」均為真(如表中的第二行所示)。對於所有其他的真值指派,該命題均為假。
現在,我們為如下命題建構一個真值表:
例11-58a (H · M)∩~B
例11-58a的真值表是:
例11-63

上述復合命題所對應的公式包含三個簡單命題:H、M和B。它們的真值的所有可能組合顯示在真值表的左側。如前面所述,我們使用2n來計算所需的行數。在這裡,n等於3,因此需要八行。然後,我們把真假值指派給左側的三個列。從最左側的那個開始(位於H下方),位於頂部的一半是T,位於底部的一半是F。然後,到了左側的中間這一列,與左側的四個T對應,得到兩個T和兩個F;與左側的四個F對應,也得到兩個T和兩個F。最後,對於左側的最後一列,依據與上述相同的劃分方法,可以得到T、F、T、F、T、F、T、F。這個約定保證了我們可以得到真值的所有可能的組合。這樣,位於最頂端的一行都是T,位於最底端的一行都是F,而位於中間的則是其他可能的組合。
當我們輸入這些值之後,再來查看右上角的那個復合命題公式。它是一個條件式。因此,它的主聯結詞是「∩」。在它的下方,將放置最終的結果(位於方框中)。但是,只有在先找到了前件H·M和後件~B的可能的真值之後,才能確定該條件式的可能的真值。那些真值構成了位於「·」和「~」下方的列。最後一步是把該條件式的真值規則應用於這兩列。
專欄11-9 復合命題的真值表
在一個真值表中,指派給左側各個簡單命題的真值數目取決於待求解的公式(位於右側上方)中出現的不同命題的數目。對於任何一個簡單命題,只有兩種可能的真值(真和假)。因此,對於像~P這樣的復合命題,只需要兩行。但是,隨著命題的增加,依據公式2n計算得來的真值數目要相應增加:當n等於2時,需要四行;當n等於3時,需要八行;當n等於4時,需要十六行,以此類推。對於例11-62,需要四行。此外,為了確保能夠得到所有可能的真值組合,我們採用如下約定:在最左側字母下方的那一列,位於頂部的一半是T,位於底部的一半是F;然後,按照前面例子中闡述的模式,自左向右指派各個列中的真值。
