正如我們在第5章看到的,任何一個具有有效形式的論證本身也是有效的,可以看作這個形式的替換例或事例。任何一個無效形式的代入例本身也是無效的。然而,命題邏輯系統具有大量的無效或有效形式。因此,僅僅通過辨識某一論證是一個有效式或無效式的例示是不可能學到命題邏輯系統中論證的有效性或無效性知識的。但能夠辨識一些最常見的有效式或無效式也是非常有益的。我們將重新考察第5章已經介紹過的五種形式,學習如何認出例示那些形式的論證。
肯定前件式
肯定前件式是一種常見有效式,它的一個前提是條件句,另一個前提是條件句前件的肯定,結論是後件的肯定。如,
例12-10 1. 如果喬斯是消防員,那麼他就為消防隊工作。
2. 喬斯是消防員。
3. 喬斯是為消防隊工作。
這個論證舉例說明了「肯定前件式」(字面意義是「肯定的模式」)這一有效式,其符號表示是,
例12-10a 1. P∩Q
2. P
3. Q
因為實質條件句的前件表達的是後件的充分條件,前件在肯定前件式中被斷定為真,任何具有這一形式的論證都有效。換句話說,如果P蘊涵Q為真,並且P為真,那麼Q必然為真。具有這一形式的論證的有效性可以通過真值表例12-11證明。
例12-11

可以看出,這個真值表中並沒有兩個前提都真,但結論為假的行。
否定後件式
另一常見的有效形式是否定後件式(字面意思是「否定的模式」)。如果一個論證包含兩個前提,一個是條件句,另一個是對條件句後件的否定,那麼這個論證就是否定後件式的代入例。結論是對條件前提的前件的否定。如,
例12-12 1. 如果銅是一種稀有金屬,那麼就很昂貴。
2. 銅並不昂貴。
3. 銅不是稀有金屬。
這個論證的形式是否定後件式,可表示如下:
例12-12a 1. P∩Q
2.~Q
3.~P
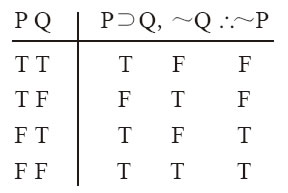
實質條件句中,後件表達的是前件的必要條件。如果Q對P是必要的,那麼若非Q,則非P。換句話說,否定一個前提的後件可以推出否定其前件。如下表表明,任何否定後件式的代入例都是有效的:
例12-13
換質位
換質位論證的前提是一個單稱的條件句,結論不僅交換了條件句前後件的位置,而且改變了前後件的質,這個論證具有的就是換質位形式。如,
例12-14 1. 如果安娜是一名革命者,那麼她就反對建立秩序。
2. 如果安娜不反對建立秩序,那麼她就不是一名革命者。
例12-14的形式正是換質位,因為:
例12-14a 1.P∩Q
2.~Q∩~P
例12-14a使我們認識到,因為例12-14的形式有效,所以論證本身也是有效的。為什麼有效?與否定後件式類似:因為Q是實質條件句的後件,是其前件P的必要條件。因此,如果Q假,P一定假。換質位的有效性可由下列真值表表明:
例12-15

假言三段論
之所以稱假言三段論,是因為這種論證有兩個前提(與三段論相同),而且其前提(和結論)都是假言或條件命題。如:
例12-16 1. 如果伊萊恩是新聞報道者,那麼她就是記者。
2. 如果她是記者,那麼她就知道如何寫作。
3. 如果伊萊恩是新聞報道者,那麼她就知道如何寫作。
其形式如下:
例12-16a 1. P∩Q
2. Q∩R
3. P∩R
例12-16a使我們明白,例12-16具有假言三段論這一有效形式。
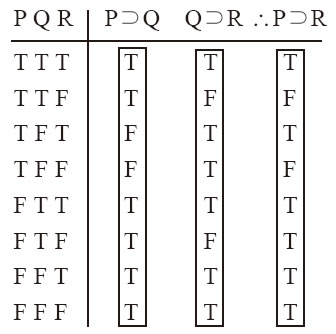
仔細考察這個形式就會發現前提1的後件是前提2的前件,而前提1的前件與前提2的後件分別是結論的前件和後件。顯然,因為條件命題的前件表達的是後件的充分條件,Q又是P的充分條件,這可以推出P是R的充分條件。例12-16是這個形式的代入例,因此是有效的。下列真值表可以表明假言三段論的有效性:
例12-17
析取三段論
最後,我們要討論一種不涉及條件前提的有效論證形式:析取三段論。之所以稱析取三段論,是因為它有兩個前提(與三段論相同),並且其中一個是析取式。一個前提表達的是析取式,另一個是對析取式的一個析取支的否定,這可以導出結論是另一個析取支的肯定。如:
例12-18 1. 我的汽車要麼是被警察拖走了,要麼是被偷了。
2. 我的汽車並沒有被警察拖走。
3. 我的汽車是被偷走了。
例12-18是析取三段論的一個代入例。由於否定的析取支不同,析取三段論又可以分為以下兩種形式,它們之一可以精確地刻畫例12-18:
例12-18a 1. PˇQ 例12-18b 1. PˇQ 2. ~P2. ~Q 3. Q 3. P 因為例12-18否定的是析取前提的第一個析取支,所以正確形式應是例12-18a。但無論是哪種形式,根本原則是:已知相容析取的真值函項定義,如果相容析取前提為真,但其中一個析取支為假,就可以推出另一個析取支為真。因此,正如下列真值表可以證明,任意具有例12-18a或例12-18b形式的論證都有效:
例12-19

更複雜的有效代入例
當著手分析命題邏輯系統中的論證時,能夠辨識上述五種基本的有效形式將是非常有益的。只要某個論證具有上述形式之一,它就有效,不需要進一步的程序!一個論證有效,只要其前提和結論所反映的形式有效即可。這就意味著一個有效論證的前提和結論除主要反映有效形式中的前提和結論之外,還在描述聯結詞方面起到了十分重要的作用。只要形式和論證的主聯結詞完全相同就沒有問題。以下是我們在判定某一論證具有何種形式時需要識記的幾點內容:
(1)一個具體論證,其前提的順序與它本身是否具有肯定前件、否定後件、假言三段論或析取三段論形式這一問題無關。
(2)聯結詞除標準的表述之外,還有其他表述方式。
(3)雙重否定可以消去。因此,任何不包含否定的命題都可以解釋為具有雙重否定的命題。
(4)一個有效論證除與基本的有效形式中的主聯結詞對應之外,還要與形式中的其他部分對應。
下列論證可以說明(1)和(3):
例12-20 如果跳蚤是微生物,那麼就是裸眼不可見的。但跳蚤是裸眼可見的,因此,它們不是微生物。
例12-20這個論證是否定後件式的代入例:
例12-20a 1. E
2. M∩~E
3.~M
依據(3),前提1中的E等價於~~E,即2的後件──~E的否定。而結論3是對前件的否定。依據(1),這正是否定後件式!
以下論證可以例證(2):
例12-21 1. 只有空襲結束,軍艦才可以起航。
2. 空襲沒有結束。
3. 軍艦不能起航。
一旦使用「如果……那麼」這樣的標準形式替換「只有……才」,那麼例12-21顯然是否定後件式的代入例,論證形式是:
例12-21a 1. C∩O
2.~O
3.~C
為什麼例12-21的第一個前提可以表示為H∩L的形式?因為「只有……才」是條件句的另一種日常語言表達方式。例12-21中,條件句的前件是「只有」命題之後的命題,後件就是「只有」命題。回顧第11章所講的復合命題,溫習真值函項聯結詞不同表達方式的知識。但是,還有另一個與(1)相關的例子,這次是用「除非」而不是「或者」表達析取。一旦知道什麼詞與「除非」等價,就能辨識例12-22、這個析取三段論的形式是例12-22a:
例12-22 1. 喬治今晚會看《辛普森一家》,除非他去踢球。
2. 他今晚不踢足球。
3. 喬治今晚會看《辛普森一家》。
例12-22a 1. GˇF
2.~F
3. G
與上述(1)和(3)相關的另一個例子如下:
例12-23 1. 艾迪是銀行僱員蘊涵他有工作。
2. 艾迪只有是銀行僱員,才可以是銀行支票員。
3. 艾迪是一名銀行支票員蘊涵他有工作。
前提的順序(上例是倒置)以及「蘊涵」和「只有……才」,都不妨礙把例12-23看作假言三段論的一個代入例。一旦我們按照邏輯順序排列前提,使用形如例12-23a中的符號語言表示上述論證。如例12-23所示,令E表示「艾迪是銀行僱員」,B表示「艾迪是銀行支票員」,J表示「艾迪有工作」,一旦我們依照邏輯順序重新排列前提,並把例12-23翻譯成符號語言,前述觀點就是顯然的。
例12-23a 1. E∩B
2. B∩J
3. E∩J
現在,考察以下論證以及它們的形式表徵:
例12-24 1. 哥斯達黎加是一個和平的國家,而且這個國家沒有軍隊。
2. 哥斯達黎加只有沒有公眾騷亂,才是一個和平並且沒有軍隊的國家。
3. 哥斯達黎加沒有公眾騷亂。
例12-24a 1. C ·ˇ~A
2.(C·~A)∩~N
3.~N
例12-25 1. 喬伊要麼在歐洲受審,要麼被引渡美國。
2. 喬伊要麼在歐洲受審,要麼被引渡美國,蘊涵他辯護失敗而且不是自由身。
3. 喬伊辯護失敗而且不是自由身。
例12-25a 1. JˇE
2.(JˇE)∩(D ·~F)
3. D ·~F
嚴格地從前提與結論之間的主聯結詞的角度看,上述兩個論證都是肯定前件式的代入例。因為兩個論證都由一個條件前提(恰好是第二個前提)以及條件前提前件的肯定(恰好是第一個前提)構成。一個論證中,前提的排列順序以及前提本身是包含若干聯結詞的復合命題,這兩點都不會影響整個論證成為肯定前件式的代入例。
一些標準的無效論證形式
我們已經看到,有很多種缺陷可以導致論證不成立。不同缺陷構成了所謂的謬誤,包括已經討論過的非形式謬誤。現在,我們來討論它們在命題邏輯系統中的表現形式,包括一些形式謬誤。(如圖12-1所示)
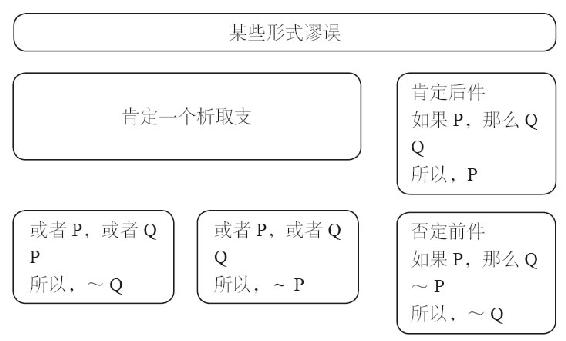
圖12-1 無效的論證形式
所有形式謬誤都與有效式非常類似,但又有某種程度上的區別。因此,它們是無效的演繹論證形式的代入例。一個論證是無效的,當且僅當具有這一形式的論證有可能前提真而結論假。為了證明一個論證形式的無效性,只需找到一個具有相同形式的論證具有真前提和假結論。如:
例12-26 1. 如果信使來了,鍾會在中午響起。
2. 鍾在中午響起。
3. 信使來了。
這個論證是無效的,因為其前提為真、結論為假是可能的。即使在有些例子中,前提和結論在某種情形下都是真的,也會存在其他情形。其中,具有相同形式的論證可能具有真前提和假結論。
假設信使沒來,但鍾確實在中午響了,儘管鍾是被鄰居敲響的。此時,例12-26的前提都為真,但結論為假。因此,當前這個情形就等價於可以顯示例12-26無效的反例。
通常在現實生活中,我們都會找到一個反例證明特定論證的無效性。但我們也可以不用反例,因為說明一個論證無效,只需描述一個「可能世界」(可以是、也可以不是現實世界──僅僅是一個內部沒有矛盾的情境)。其中,具有相同形式的論證可能具有真前提和假結論。
因此,一個論證的無效性可以通過上述方式證明:試圖描述一個可能情境,其中,當前討論的論證前提真、結論假。如果提不出這樣的情境,可以先抽像出論證形式。例12-26的形式如下:
例12-26a 1. P∩Q
2. Q
3. P
然後找到一個具有相同形式的論證,在某一可能情形中前提為真,結論為假。如,
例12-27 1. 如果貝拉克·奧巴馬是共和黨,那麼他就是一個政黨的成員。
2. 他是一個政黨的成員。
3. 貝拉克·奧巴馬是共和黨。
例12-27表明在現實世界,一個具有相同形式的論證(如例12-27)具有真前提和假結論。依據無效的定義,例12-27無效。它等價於任何具有相同形式論證的反例。
肯定後件
上述無效論證都是肯定後件式的代入例。
肯定後件謬誤是指一個論證具有一個條件句前提,另一個前提肯定了條件句的後件,其結論是對條件句前件的肯定。
肯定一個命題就等於說它為真。犯了這一謬誤的論證所肯定的是一個實質條件句的後件。後件總是表達前件的必要而非充分條件。所以,後件的真絕不能確保前件(結論)的真。以下是一個較複雜的肯定後件的示例:
例12-28 1. 如果奧爾森一家是獵鹿者,那麼,若他們打獵,則不打野雞。
2. 若奧爾森一家打獵,則不打野雞。
3. 奧爾森一家是獵鹿者。
例12-28a 1. O∩(H∩~A)
2. H∩~A
3. O
與任何肯定後件式的代入例相同,例12-28也是無效的。這一形式的無效性可通過如下真值表說明:
例12-29
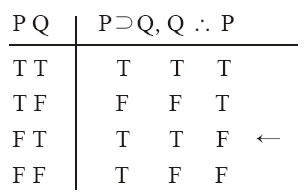
正如你能看到,這個真值表中有一行是前提都真,但結論為假。
專欄12-3 如何避免肯定後件式謬誤
在肯定前件式中,一個前提肯定的是另一個前提的前件(而不是後件),同時結論肯定的是其後件。
因此,要謹慎對待看起來像但實際上不是肯定前件式的論證,因為其條件前提的後件被另一個前提所肯定(而它的後件由結論肯定)。
否定前件式
另一個形式謬誤是否定前件式。
否定前件式是這樣一種謬誤,其中一個前提是條件形式,另一個前提是條件前提前件的否定,結論是條件前提後件的否定。
假設我們遇到了如下論證:
例12-30 1. 如果奧斯卡是波士頓交響樂團的提琴手,那麼他就懂樂譜。
2. 事實上,奧斯卡並不是波士頓交響樂團的提琴手。
3. 他不懂樂譜。
顯然,這個論證無效。「奧斯卡是波士頓交響樂管絃樂隊的提琴手」是「懂樂譜」的充分條件(如果他在該樂團,那麼就懂樂譜)。但不是必要條件,因為有很多不在該樂團中的人都懂樂譜。因此,「他不懂樂譜」不能被必然地推出。簡而言之,例12-30無效,因為它犯了否定前件謬誤。更普通地說,任何例示這一謬誤的論證都是無效的,因為否定條件前提的前件等於說前件假。但實質條件句的前件表達的是後件的充分條件:所以前件假,結論可能是真的。因此,否定條件句的前件不能推出後件的否定。上述論證就是否定前件式的代入例。任何犯了這類謬誤的論證都具有以下形式:
例12-30a 1. P∩Q
2.~P
3.~Q
否定後件的無效性可通過真值表例12-31得到說明:
例12-31
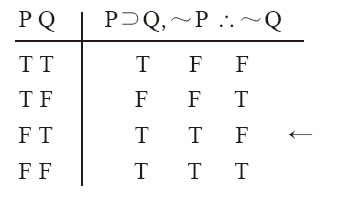
專欄12-4 如何避免否定前件式謬誤
在否定後件式中,條件前提的後件被另一個前提否定(結論正是對前件的否定)。
因此,謹慎對待看起來像但實際上不是否定後件式的論證,因為其條件前提的前件被另一個前提所否定(同時論證的結論是後件的否定)。
肯定一個析取支
另一個形式謬誤是「肯定一個析取支」。
犯「肯定一個析取支」謬誤的論證,特徵是其中一個前提是相容析取,另一個前提肯定了前者的一個析取支,結論是對另一個析取支的否定。
肯定一個析取支是無效形式,則是因為,我們是在相容意義上(即,P或者Q,或P並且Q)理解「或者」的。除兩個析取支都為假外,相容析取在其他情況下都是真的。因此,假設一個相容析取為真,否定其中一個析取支(即說它為假),可以推出另一個析取支一定為真。但肯定一個析取支(說它為真)並不能推出另一個析取支的否定,即不能推出另一個析取支為假。(在不相容析取的情況下,「肯定一個析取支」並不是謬誤)如:
例12-32 1. 我的汽車或者被警察拖走了,或者被偷了。
2. 事實上,我的汽車被警察拖走了。
3. 我的汽車沒被偷走。
兩個前提都為真的情況下,上述結論有可能為假嗎?有可能!一種可能情況是,盜竊犯在晚上撬開了汽車,然後非法停車,因此被警察拖走。如果是這種情況,例12-32的前提就都是真的,但結論為假。因此,結論並不必然地從前提推出──也是推不出的。因此,論證無效。任何具有下述一種形式的論證都會犯這樣的謬誤:
例12-32a
Ⅰ1. PˇQⅡ1. PˇQ 2. P2. Q 3.~Q3.~P 因為例12-32中的「或者……或者……」是相容析取,肯定其中一個選言支並不能推出否定另一個。從相容析取的角度看,上述兩種形式都無效。肯定一個析取支的無效性可通過下列真值表說明:
例12-33
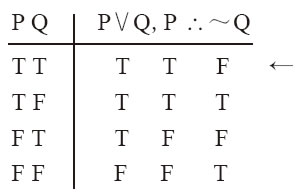
現在已經識別出了與三種形式謬誤對應的無效論證形式。如果一個論證具有上述形式之一,那麼並不需要通過真值表判定它是否有效。僅需指出這個論證具有:肯定後件、否定前件或肯定一個析取支的形式即可。如果你能區分這三種無效式和之前討論的五種有效式,那麼就會比較容易地區分無效論證和有效論證。
專欄12-5 如何避免「肯定一個析取支」謬誤
注意,析取三段論的前提否定的是另一個前提的析取支,結論肯定的是另一個析取支。
因此,要謹慎對待看起來像但實際上不是析取三段論的論證,因為其前提肯定的是另一個前提的析取支,而結論否定的是剩下的析取支。
一種證明有效性的簡明方法
上文討論的一些有效論證形式通常被用作有效性證明中的基本推理規則。這是一種程序,旨在展示一個命題邏輯有效論證的結論是如何從其前提一步一步推導出來的。假設一個論證事實上是有效的,可以通過建構一個證明顯示這一點。在準備構造這類證明之前,我們將補充一些基本的有效形式和替換規則,使我們擁有足夠多的證明所需要的推理規則。
基本原則
為了建構有效性證明,我們需要一些有效論證形式以及一些復合命題之間的等價關係。前者可以作為推理規則,使我們從一個前提或多個前提推出結論。後者可以作為替換原則,允許我們使用一個表達式替換另一個與之等價的表達式。我們的規則可表示如下:
基本的推理規則
(1)肯定前件式(MP)P∩Q,P∴Q (2)否定後件式(MT)P∩Q,~Q∴~P (3)假言三段論(HS)P∩Q,Q∩R∴P∩R (4)析取三段論(DS)PˇQ,~P∴Q (5)簡化律(Simp)P · Q,∴P (6)合取律(Conj)P,Q∴P · Q (7)附加律(Add)P∴PˇQ 基本的替換規則
(8)換質位(Contr)(P∩Q)≡(~Q∩~P) (9)雙重否定(DN)P≡~~P (10)德摩根律(DeM)~(P · Q)≡~Pˇ~Q ~(PˇQ)≡~P ·~Q (11)交換律 (Com)(PˇQ)≡(QˇP) (P · Q)≡(Q · P) 12)實質條件的定義(Cond)( (P∩Q)≡(~PˇQ) (13)是指等價的定義(Bicond)(P≡Q)≡〔(P∩Q)·(Q∩P)〕 (P≡Q)≡〔(P · Q) ·(~P∩~Q)〕什麼是有效性證明
有效性證明可以是形式的,也可以是非形式的。在一個形式化的有效性證明中,推出關係是指在一個邏輯系統內部嚴格獲得的某些合式公式之間的關係,這些公式不必具有一個自然語言(英語、葡萄牙語或普通話)解釋。而且,形式證明所使用的基本推理和替換規則可以證明任意從命題邏輯有效論證的前提推出的結論。另一方面,非形式證明中的推出關係是自然語言可表達的特定命題之間的關係。如果推出的證明僅涉及公式,那麼可以假設在那些公式中有一個自然語言的解釋。另外,使用非形式方法的基本規則不能為所有命題邏輯有效的論證提供一個有效性證明。
儘管我們為了方便,在構造一些論證的有效性證明時使用的是符號語言,但可以假設那些論證都有一個自然語言解釋。對於自然語言表達的有效論證,首先把它翻譯為符號語言。然後使用上述規則證明它們的有效性。這些規則可以用於證明許多論證的命題邏輯有效性,下文將會討論如何使用規則證明有效性。
無論形式方法還是非形式方法,所有有效性證明都要求在對前提使用一個或多個推理和替換規則之後,原則上是可以推出結論的。這些規則被公認是「基本」的。(因為這個系統內的任何證明都至少需要預設幾個基本的、在本系統內不能證明的規則)
如何構造一個有效性證明
現在使用上述基本規則證明下列論證的有效性:
例12-34 愛麗絲和卡洛琳將都在明年畢業。但如果卡洛琳明年畢業,那麼吉賽爾就會獲得獎學金,當且僅當愛麗絲明年畢業。因此,要麼吉賽爾會獲得獎學金,當且僅當愛麗絲明年畢業,要麼海倫會是致告別辭的優秀畢業生。
首先把這個論證翻譯為如下符號語言:
例12-34a A · C,C∩(G≡A)∴(G≡A)ˇH
現在可以證明這個論證的結論,(G≡A)ˇH可從前提推出。如何證明?僅對例12-34a的前提應用基本的推理和替換規則。從例12-34a的前提演繹出結論的四個步驟(3、4、5、6)分別是:
例12-34b
1. A · C 2. C∩(G≡A)∴(G≡A)ˇH 3. C·A1──交換律 4. C3──簡化律 5. G≡A2、4──肯前式 6.(G≡A)ˇH5──附加律 第3行是對前提1使用交換律(參看上述交換律規則),從而演繹出C · A。每演繹出一個公式,都要在右邊註明依據。如這個例子,表達依據的語詞包括「從」、「且」、「通過」,下文將省略(從)或使用標點替換(「且」和「通過」)。書寫依據時要注意兩點:(1)標明應用特定規則的前提序號(若多於一個,則按順序寫);(2)闡明所用到的規則名稱。如果證明了某一公式,那麼可以把它看作新前提,標明序號。因為第3行的C · A已經從論證的前提演繹出來了,那麼就可以用於進一步證明的前提。事實上,它在第4行被用作導出C的依據。第5行,前提2和4通過肯前式導出了G≡A。第6行,使用附加律導出了結論,從而證明了例12-34的有效性。如此,例12-34的有效性得證。
證明和真值表
正如我們在真值表中所看到,一個論證前提和結論的真值是與論證有關的真值函項聯結詞的規則賦予的。儘管這裡只定義了五種真值函項聯結詞,但事實上,它們的總數是16個。這個數目是固定的。與之不同的是,可用於構造有效性證明的有效式和邏輯等價表達式的實際數目會因演繹系統的不同而不同。另外,證明程序並不規定從前提正確演繹出結論的步驟數:它取決於前提與我們決定採用的基本規則。
因為在這些方面,證明有一定的靈活性,所以在一個由基本規則構成的系統中,對於特定論證可以構造不止一個正確的有效性證明。也就是說,與真值表不同,一個證明並不總能在固定步驟內得出一個結論的機械程序。除此之外,為特定有效論證構造證明時,我們可能錯誤地評價了它的有效性。有可能當時「沒有看出」使用特定規則可以從前提演繹出結論,錯誤地認為論證無效。這就是為什麼,任意有效論證在「原則上」有一個有效性證明。然而必須承認,證明在某一方面確實優於真值表:當一個論證涉及很多種命題時,真值表往往會很長而且很不方便。證明就不會有這樣的問題。